時計算(基礎編)
今回は時計算です。時計算では、時計の長針と短針でつくられる角度が問題になります。いつも見慣れている時計についての問題ですが、混乱しやすいので、基礎からゆっくり説明します。今回は基礎の部分です。ちなみに、時計算で登場するのはアナログ時計です(デジタル時計ではありませんよ。念のため・・・。)
準備体操
(1) 時計の長針が1時間に進む角度は何度ですか。
(2) 時計の長針が1分間に進む角度は何度ですか。
(3) 時計の短針が1時間に進む角度は何度ですか。
(4) 時計の短針が1分間に進む角度は何度ですか。
解法
(1) 時計の長針は1時間で1周するから、360度進むことになります。
(2) 時計の長針は1時間(=60分)で1周(360度)動くから、1分間では、
360÷60=6
となり、毎分6度だけ進んでいることになります。 (3) 時計の短針は1時間あたり、1周(360度)を12等分した角度(5分刻みの大きな目盛1つ分)を進むことになるから、
360÷12=30
となり、毎時30度だけ進んでいることになります。
(4) 時計の短針は1時間(=60分)で30度(5分刻みの大きな目盛1つ分)動くから、1分間では、
30÷60=0.5
となり、毎分0.5度だけ進んでいることになります。
長針は1時間で360度1分間では6度進む(小さな目盛1つぶん)
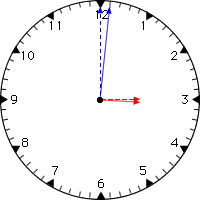
【例】 3時0分(点線)から 3時1分(実線)に 動くとき
短針は1時間で30度(大きな目盛1つぶん)
1分間では0.5度進む
答え:(1)360度 (2)6度 (3)30度 (4)0.5度
問題1
次の(1)~(5)について小さい方の角度を求めなさい。
(1) 3時ちょうどのとき、長針と短針は何度離れていますか。
(2) 3時1分のとき、長針と短針は何度離れていますか。
(3) 3時2分のとき、長針と短針は何度離れていますか。
(4) 3時3分のとき、長針と短針は何度離れていますか。
(5) 長針は短針に1分間につき、何度ずつ近づいていることになりますか。
解法
(1) 3時0分
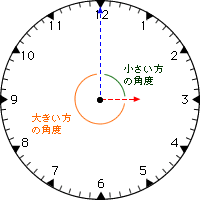
3時ちょうどのときは、長針と短針は90度だけ離れています(小さい方の角度)。
5分刻みの大きな目盛(30度)が3つ分ですね。
ちなみに、大きいほうの角度は270度です。
答え:90度
(2) 3時1分

3時ちょうどの針の位置を長針と短針のそれぞれの基準線(左図の点線)とします。 3時1分のときは、長針は基準線から6度進み、短針は0.5度だけ進みます。 そのため、3時1分には、長針は基準線の角度(90度)を6度小さくするほう(内側)に動き、短針は基準線の角度を0.5度大きくするほう(外側)に動いたことになります。
よって、3時1分のときの角度は、 90度-6度+0.5度=84.5度 この84.5度が3時1分の角度です。
答え:84.5度
(3) 3時2分

3時2分のときは、長針は基準線から12度進み、短針は1度だけ進みます。
そのため、3時2分には、長針は基準線の角度(90度)を12度小さくするほう(内側)に動き、短針は基準線の角度を1度大きくするほう(外側)に動いたことになります。 よって、3時2分のときの角度は、
90度-12度+1度=79度
この79度が3時2分の角度です。
答え:79度
(4) 3時3分
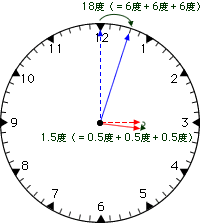
3時3分のときは、長針は基準線から18度進み、短針は1.5度だけ進みます。
そのため、3時2分には、長針は基準線の角度(90度)を18度小さくするほう(内側)に動き、短針は基準線の角度を1.5度大きくするほう(外側)に動いたことになります。
よって、3時3分のときの角度は、
90度-18度+1.5度=73.5度
この73.5度が3時2分の角度です。
答え:73.5度

このように、時計算では、長針と短針の基準を決めて考えます。どこを基準にするかは自由です。考えやすいところを基準にします(普通は大きな目盛1から12のどれか)。
そして、基準線のつくる角度に対して、長針と短針がどちらの向きにどれだけ動いたかを考えて、たしざんとひきざんで計算します。
また、次のように、基準線を一つ(たとえば12の目盛)にする考え方もあります。
3時3分のとき
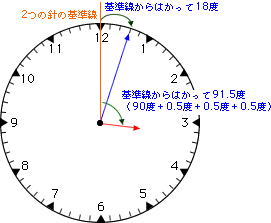
3時3分の角度は 91.5度-18度=73.5度
見方を変えると、次のように理解できます。
長針さんがスタート地点から18mのところにいて、短針さんが91.5mのところにいるとすると、
2人の差は91.5m-18m=73.5mになります。角度でも同じことです。
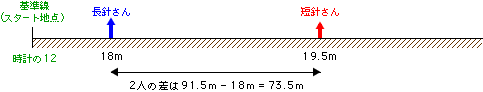
(5) 長針は毎分6度、短針は毎分0.5度進むから、5.5度が正解です(これは旅人算と同じ考え方です。動く物が針で、道のりは角度にあたります)。
ためしに、(1)~(4)の答えをまとめてみます。

離れている角度は1分ごとに5.5度ずつ小さくなっていることがわかります。つまり、長針は短針に1分間につき、5.5度ずつ近づいているのです。
これは、3時に限らず、いつの時間でも同じです。長針が短針に追いついて遠ざかるときも同じで、1分間につき5.5度ずつ、遠ざかります。
答え:5.5度

時計算のポイント
1)長針は1分間に6度進む
2)短針は1分間に0.5度進む
3)長針は短針に1分間に5.5度近づく(遠ざかるときも同じ)
※3は旅人算と同じ考え方です
問題2
10時28分のとき、時計の長針と短針の作る角度のうち、小さいほうの角度を求めなさい。
解法
長針の基準線を大きな目盛の6、短針の基準線を大きな目盛の10とします。
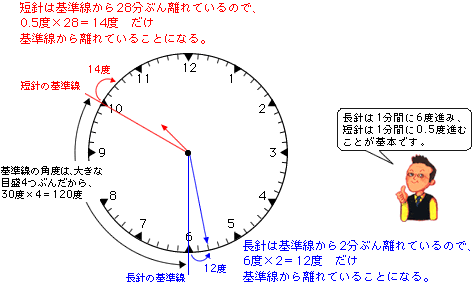
基準線の角度は、大きな目盛4つぶんだから、
30度×4=120度
長針は基準線の角度(120度)を12度ぶん大きくするほう(外側)にあり、短針も基準線の角度(120度)を14度ぶん大きくするほう(外側)にあるから、10時28分のときの角度は、
120度+12度+14度=146度
この146度が10時28分の角度です。
答え:146度

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事