学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
年令算
今回は年令算です。年令算は線分図という図を書いて解きます。年令を線で表して、過去や未来の年令を表すために線を伸ばしたり縮めたりします（ここでは、便宜上、棒で表して説明します）。少し難しく、最初は読んでも理解できないかもしれませんが、あきらめずに図が何を意味しているのかをじっくり考えてみてください。
考え方のポイントは年令の差です。年令の差は何年たっても変わらないという性質を利用して問題を解きます。年令の差が何と等しくなるかを考えながら読んでみてください。
問題1
現在、母は28才、子は4才です。母の年令が子の年令の4倍になるのは、今から何年後ですか。また、そのときの母と子の年令はそれぞれ何才ですか。
解法
現在
次のように現在の年令を線（ここでは棒）で表します。母と子の年令の差は24才です。
○年後（母の年令が子の年令の4倍）
その○年後は、母も子も○才年をとるので、棒が○年分のびます。
ここでも、母と子の年令の差は24才です。
母の年令が子の年令の4倍だから、差の24の中に4＋○が3つ入ることになります。
そのため、4＋○の1つ分は8になります（24÷3）。
だから、○は4になります（8－4）。
答え：4年後、母は32才、子は8才
なんとなく、わかったような、わからないような・・・という人は、実際に身近な人にあてはめて、ためしてみると実感がわくと思います。
問題2
現在、おじいさんは72才、おとうさんは42才です。おじいさんとおとうさんの年令の比が2：1であったのは、何年前ですか。また、そのときのおじいさんとおとうさんの年令はそれぞれ何才ですか。
解法
現在
次のように現在の年令を線（ここでは棒）で表します。おじいさんとおとうさんの年令の差は30才です。
○年前（おじいさんとおとうさんの年令の比が2：1）
その○年前は、おじいさんもおとうさんも○才若いので、棒が○年分ちぢみます。
ここでも、おじいさんとおとうさんの年令の差は30才です。
おじいさんとおとうさんの年令の比が2：1（おじいさんの年令の半分がおとうさんの年令）です。
すると、差の30の中に42－○が1つ入ることになるから、42－○の1つ分は30になります。 だから、○は12になります（42－30）。
答え：12年前、おじいさん60才、おとうさん30才
問題3
姉は3300円、弟は2300円持っています。二人が同じ金額を出し合って、母の日のプレゼントに花たばを買ったので、姉と弟の残金の比が5：3となりました。姉と弟はいくらずつ出し合って、いくらの花たばを買ったのでしょうか？
解法
プレゼントを買う前
次のように姉と弟の持っている金額を線（ここでは棒）で表します。
姉と弟の金額の差は1000円です。
プレゼントを買った後（姉と弟の残金の比が5：3）
同じ金額○円ずつ出し合って、プレゼントを買ったとします。
同じ金額○円ずつ出し合って、プレゼントを買ったので、それぞれ棒が○円分ちぢみます。
同じ金額○円ずつ出し合ったので、買ったあとでも姉と弟の金額の差は同じく1000円です。
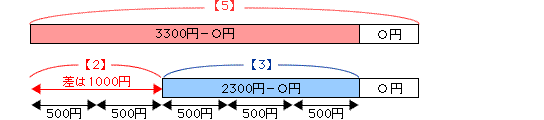
姉と弟の残金の比が【5】：【3】なので、差の【2】は1000円に相当します。
すると、1はその半分の500円になります。
さらに【3】の部分の 
は1500円に等しくなるので、
○円は、800円で、プレゼントは1600円となります。
答え：800円ずつ出し合って、1600円の花たばを買った。
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
