約束記号(演算記号)
今回は約束記号(演算記号)に関する問題です。普段よく使っている+-×÷の記号の他に、○、▼、□など記号が登場します。問題によって登場する記号の種類も記号の約束も違います。
解き方のポイントは、それらの記号が表す約束をみつけて、約束通りに素直に計算することです。そして、約束通りに計算しながら○、▼、□などの見慣れない記号は、どんどん減らしていきます。
記号が表す約束は問題文に示されていることもありますが、問題の(例)から自分で見つけなければならないこともあります。自分で見つけなければならない問題では、多少センスが必要かもしれませんが、それは問題を多く解くことにより養われていきます。
問題1
A○B=A×A-A×Bと約束します。このとき、次の計算をしなさい。
(1)5○2
(2)(99○98)○97
解法
解き方のポイントは、最初に述べた通り、
①約束をみつけて、約束通りに素直に計算すること
②約束通りに計算しながら○、▼、□などの見慣れない記号は、どんどん減らしていく。
ということでした。
①の約束は問題文に書かれているので、みつける必要はありません。素直に計算していきましょう。
(1) 5○2
= 5×5-5×2 ←約束通りに計算
= 25-10
= 15
(2) (99○98)○97
まず( )の(99○98)を計算します。
(99○98) = 99×99-99×98 ←約束通りに計算
= 9801-9702
= 99
このように計算すると少し大変です。
99×99は99を99回たした数
99×98は99を98回たした数
です。99を99回たした数から99を98回たした数をひくので、99が1つ残ると考えることができます。この考え方ができれば、暗算ですばやく、しかも正確に計算することができます。これは、分配の法則の考え方です。
(99○98)
↑99 ○97 = 99○97
= 99×99-99×97 ←約束通りに計算
= 9801-9603 = 198
これも分配の法則の考え方が使えます。
99×99-99×97
=99×(99-97)
=99×2
=198
と計算できます。
答え:(1)15 (2)198
問題2
次の▼と◇は、それぞれ一定の規則で計算する記号とします。例に従って、あてはまる数を求めなさい。
(例)
0▼3=3、 1▼3=5、 2▼3=7、 5▼0=10、 5▼1=11、 5▼2=12
2◇3=1、 3◇3=3、 4◇3=5、 3◇0=6、 3◇1=5、 3◇2=4
(4▼9)◇(7◇6)=□
解法
解き方のポイントは、最初に述べた通り、
①約束をみつけて、約束通りに素直に計算すること
②約束通りに計算しながら○、▼、□などの見慣れない記号は、どんどん減らしていく。
でした。
この問題では、約束が問題文に書かれていないので、(例)を見て、自分でみつけなければなりません。
A▼B=A+A+B ・・・A×2+Bでも同じ
A◇B=A+A-B ・・・A×2-Bでも同じ
となっていることがわかります。

なかなか見つからない場合は、それぞれの例で、数が共通している箇所や規則的に増えているところに注目すると約束がみつけやすくなります。たとえば、▼の前の5が共通で、▼の後ろが1ずつ増え、それにともない=10、=11、=12と1ずつ増えていることに注目しながらみつけます。
5▼0=10、 5▼1=11、 5▼2=12
約束がみつかったら、素直に約束通りに計算するだけです。
まずは、(4▼9)◇(7◇6)の( )の(4▼9)と(7◇6)に分けて計算してみます。

答え:26
問題3
AをB回かけるとCになることを、A◎C=Bと表すことにします。
たとえば、5◎25=2、 2◎16=4 となります。
このとき、次の(1)~(3)の□にあてはまる数を答えなさい。
(1)3◎27=□
(2)(2◎32)+(2◎□)=2◎128
(3)(5◎125)-(3◎9)=□◎4
解法
ここでもポイントは、もちろん同じですが、約束が少し難しいので、混乱しないようにゆっくり考えてゆきましょう。
①約束をみつけて、約束通りに素直に計算すること
②約束通りに計算しながら○、▼、□などの見慣れない記号は、どんどん減らしていく。
約束は問題文に書かれているので、◎を減らす方針で、約束通りに計算していきましょう。
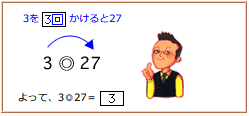
(1) 3◎27=
3を 回かけると27になるということだから、
回かけると27になるということだから、
 は3になります(3×3×3=27)。
は3になります(3×3×3=27)。
(2) (2◎32)+(2◎  )=2◎128
)=2◎128
式が少し複雑なので、計算できるところを約束通りに計算して、◎を減らしていきましょう。
まず、2◎32は、2を何回かけたら32になるかを考えます。
2×2=4
2×2×2=8
2×2×2×2=16
2×2×2×2×2=32
だから、2を5回かけると32になります。
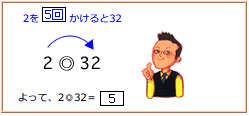
つまり、2◎32=5(回)です。
次に、2◎128は、2を何回かけたら128になるかを考えます。先の続きで、
2×2×2×2×2×2=64
2×2×2×2×2×2×2=128
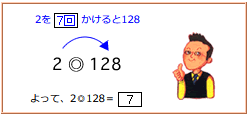
だから、2を7回かけると128になります。
つまり、2◎128=7(回)です。
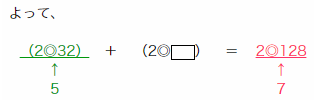
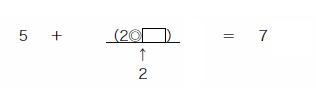
これより、(2◎  )は2にならなくてはいけないので、
)は2にならなくてはいけないので、
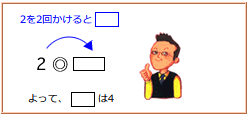
2◎  =2
=2
 は2を2回かけた数だから
は2を2回かけた数だから  は4
は4
(3) (5◎125)-(3◎9)=  ◎4
◎4
これも、計算できるところから、約束通りに計算していきます。
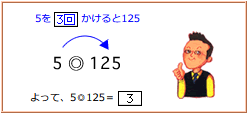
まず、(5◎125)は、5を何回かけると125になるかを考えます。
すると、5×5×5=125
だから、5◎125=3(回)です。
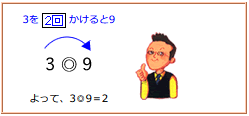
同じように、(3◎9)は、3を何回かけると9になるかを考えます。
すると、3×3=9
だから、3◎9=2(回)です。
よって、

3-2=  ◎4
◎4
1=  ◎4
◎4
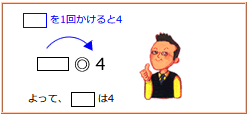
つまり、  ◎4=1で、
◎4=1で、
これは  を1回かけると4になるということだから、
を1回かけると4になるということだから、
 は4です(4を1回かけると4になる)。
は4です(4を1回かけると4になる)。
答え:(1)3 (2)4 (3)4

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
