鶴亀算(つるかめざん)

かつて鶴亀算に悩まされたお父さん、お母さんも多いのではないでしょうか? 今でも鶴亀算は、子どもたちにとって苦手な問題の一つです。 名物塾講師、きんたろう先生ならどう教えてくれるでしょうか?
準備体操
鶴と亀が合わせて6 匹います。足の合計が2 0 本であった。 鶴と亀はそれぞれ何匹いますか? (鳥は1 羽2 羽と数えますが、ここでは「匹」としておきます)
解法
これが代表的な鶴亀算の問題です。子ども達にとっては好き嫌いがかなり分 かれるようです。嫌いな子の意見を聞いてみると、鶴と亀が混在している 様子をイメージしていまい、しかも鶴と亀で足の数が違うので、混乱して しまうようです。そこでまず、すべて鶴であったときの単純な場合をイメージしながら考えてみましょう。今回は鶴亀算をこんな風に教えるとわか りやすいのではという一例を示しておきます。

まず、合計6 匹すべてが鶴とします。 が2本足の鶴を表しているものとして、 図に書いて見ましょう。すると、足の数が、合計12 本で8 本足りないことがわかります。 なぜ足りないかというと、亀が前足を引っ込めて、2本足の鶴に成りすましているからです。
が2本足の鶴を表しているものとして、 図に書いて見ましょう。すると、足の数が、合計12 本で8 本足りないことがわかります。 なぜ足りないかというと、亀が前足を引っ込めて、2本足の鶴に成りすましているからです。
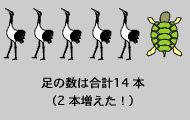
それでは、1 匹の亀さんに前足を出してもらいましょう。 を4本足の亀を表しているものとして、図に書いてみます。
を4本足の亀を表しているものとして、図に書いてみます。
足の数は合計14 本になり、2 本増えましたが20 本にはまだ足 りません。 さらにもう一匹の亀さんに足を出してもらいます。

足の数は合計16 本になり、20 本にはまだ足 りません。 さらにもう一匹の亀さんに足を出してもらいます。

足の数が20 本まで、もう少しです。同じようにして、合計20 本になるまで、亀さんたちに足を出してもらいましょう。

これで鶴に成りすましていた亀さん全員に足を出してもらい、合計20 本になりました。ここで、亀が1 匹増えると、足の数が 2 本増えるということは大変重要です。鶴亀算応用問題の考え方のポイントになります。答えは、図から わかるように、鶴は2 匹、亀は4 匹です。このように、最初はすべてが鶴として足の数を考えていくと、鶴亀算は解けるのです。 逆に最初すべて亀として、足の数を減らしていく考え方でもOKです。
答え
鶴が2 匹、亀が4 匹
一般的な解き方
6×2 =12 …6 匹すべてを鶴とすると、足は12 本。
20-12 =8 …足の数は合計で20 本だから、8 本少ない。
8 ÷2 =4 …亀を1 匹増やすと足の数が2 本増えるから、亀を4 匹増やせば、不足の8 本が解決!よって、亀は4 匹。
6-4 =2 …鶴と亀の合計が6 匹で亀が4 匹なので、鶴は2 匹。
いかがでしょうか、よくわからないと言われている鶴亀算も図でイメージすれば、簡単に解けるのです。
問題1 難易度 ★
鶴と亀が合計8 0 匹います。足の数の和が2 0 0 本であったとき、鶴と亀はそれぞれ何匹いますか?
解法
80 匹すべてが鶴とすると、足の数は80 ×2 =160 本。
足の数の和は200 だから、200-160 =40 で、40 本足りない。
亀を1 匹増やすと2 本ずつ足が増えていくから、40 ÷2 =20 匹の亀がいることになる。鶴は80-20 =60匹。
答え
鶴が6 0 匹、亀が2 0 匹
いかがでしょうか? 一般的には鶴亀算とは、全体の数や量がわかっているとき、個々の数や量を求める計算なのです。それでは、次に鶴亀算の応用問題を解いてみまし ょう。
問題2 難易度 ★★
5 0 円切手と8 0 円切手を合計1 4 枚買って1000 円を支払いました。 5 0 円切手と8 0 円切手をそれぞれ何枚買ったのでしょうか。
解法
これも、実はかくれ鶴亀算です。先ほど述べた通り、全体で1000 円とい うことがわかっていて、個々の切手の枚数を求める問題だからです。 50 円切手を鶴、80 円切手を亀に相当させて考えて見ましょう。
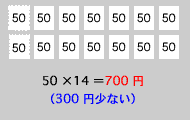
まず、すべて50 円切手を買ったとします。すると、合計700 円になるので、1000 円より300 円少ない ことになります。そこで、80 円切手を1 枚ずつ増やしてみましょう。

80 円切手を1 枚増やすと
(50 ×13 )+(80 ×1 )=650 +80 =730 円(30 円増えた!)

80 円切手を2枚増やすと

80 円切手を3 枚増やすと
このように80 円切手を1 枚ずつ増やすと、合計が30 円ずつ増えていくのです。(鶴と亀の場合は、鶴が亀になると2 本ずつ増えましたね)それでは、何枚増やせばよいかというと、 不足額は300 円なので、300 ÷30 =10枚。よって、 80 円切手は10 枚。合計で14 枚買ったのだから、 50 円切手は、14-10 =4 で4 枚買ったことになります。
答え
5 0 円切手4 枚、8 0 円切手1 0 枚
問題3 難易度 ★★★
次 のルールでカードゲームを2 人で行いました。 (ルール)じゃんけんで勝てば、相手から2 枚のカードをもらう。 負ければ1 枚渡す。 私 は最初10 枚のカードを持っており、7 回じゃんけんを行ったら私 のカードが15 枚になっていました。私は何回勝ち、何回負けたでし ょうか。ただし、引き分けはありませんでした。
解法
「ルール:じゃんけんで勝てば、相手から2 枚のカードをもらう。負ければ1 枚渡す。」
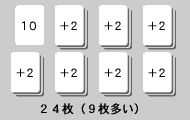
まず、7 回とも勝ったとすると、2 ×7 =14 枚のカードが増え、合計10 +14 =24 枚になっているはずです。
これを図に表すと、
15 枚と比べて、9 枚多いですね。
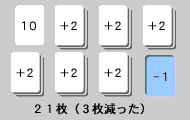
それでは、負けを1 回増やしてみましょう。
3 枚減りました。

もう1 回負けを増やしてみましょう。
さらに、3 枚減りました。
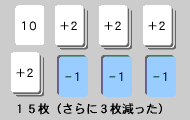
もう1 回負けを増やしてみましょう。
もう、おわかりですね。1 回負けを増やすと3 枚減るのです。
すべて勝ちとすると、9 枚多くなるので、負けを3 回増やせば、この9 枚が解決します。だから、負けは3 回です。
合計7回行ったから勝ちは4 回。
答え
勝ちは4回、負けは3回
教え方のヒント
今回も「抽象的なものを具体的に」という方針で説明しました。
この鶴亀算ですが、ご存知の通り、方程式の 考え方でも、面積図の考え方でも解けます。ただし、最初からその方法で教えると、ただでさえ、鶴と亀の足が混在して混乱している子にとっては、鶴や亀がχyや面積に化けてしまったということで、ますます混乱し、数 学から遠ざかってしまうことでしょう。
ここで説明した解き方で精一杯という子も少なくありません。まずは、 この原始的な解き方だけで、練習させるとよいでしょう。そして十分に慣れた頃、方程式や面積図を使い、まるで魔法を使ったかのように、あっという間に解けてしまうことを実践して見せると、子供達は興味を持つことしょう。
その際、例えば面積図で教える場合、初めからすべてを教えてしまうことは、考える力を損なってしまいます。 まずは、図だけを描きそれが何を意味しているのかを自力で考えさせます。そして、面積図が、自分が今まで解いてきた方法に対応していることに、自力で気がつかせることができれば大成功です。
私はゆとり教育に賛成するわけではありませんが、子供達に十分に考える時間を提供し、わかったときの喜びを経験させてあげることが、学問の入り口へ導いてあげることに繋がると思っています。

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
