一列に並べる問題

早速、特別な解き方で説明します。準備として、5枚のカードを1枚ずつ入れる5つの箱を準備します。この箱の中に1枚ずつカードを入れていきます。

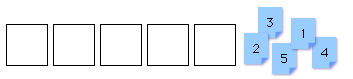
たとえば、次のように入れます

5、1、4、3、2これも並べ方の一つの方法です。他にもいろいろな入れ方（並べ方）がありますが、全部の入れ方（並べ方）を調べていては大変です。そこで、次のように順に1枚ずつ入れていく方法で考えます。

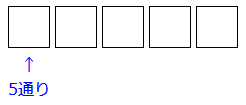
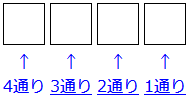
まず、一番左端の箱に、カードを1枚入れます。このときには、1から5の5枚のカードが手元にあります。そのどれを入れてもよいので、5通り（1か2か3か4か5）の入れ方があります。そこで、右の図のように 5通りと箱の下に書きます。

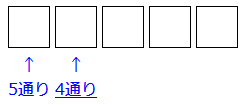
次に、左から2番目の箱にカードを入れます。そのときには、左端の箱に入った1枚のカードを除いた4枚のカードが手元にあります。その4枚のうちのいずれかを入れることになるので、4通りの入れ方があります。そこで、右の図のように 4通りと箱の下に書きます。

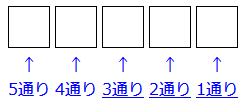
同じように、3番目の箱、4番目の箱、 5番目の箱と順に考えていくと、右の図のように、 3通り、2通り、1通りとなります。

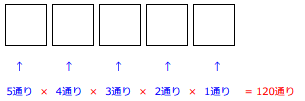
これで完成です。あとは、下に書いた○通りの○の数をすべてかければ、答えがでてしまうのです。
つまり、
5×4×3×2×1＝120（通り）
が正解です。

答え：120通り

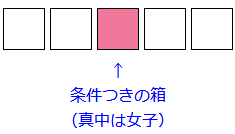
この問題も5人を並べるので、5つの箱を準備します。そして、1人ずつ順番に箱の中に入っていくことを考えます。ただし、この問題では、「女子が真中」という条件があります。このように条件がある場合は、条件のある箱を最優先で考えます。ここでは、真中の箱です。

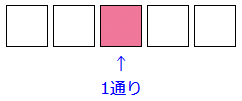
まず、女子は1人しかいないので、条件のある真中の箱は、 1通りとなります。

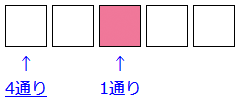
次に男子4人を考えます。どこから考えてもよいのですが、ここでは、左端の箱から順に考えていくことにします。
左端の箱には、男子4人のうち、誰か一人が入るので 4通りです。

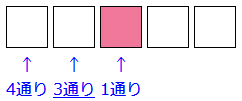
次に左から2番目の箱には、残った男子3人のうち誰か一人が入るので、 3通りです。

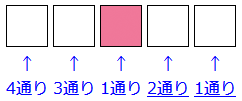
同じように残った箱を考えると、この図のように、 2通り、1通りとなります。

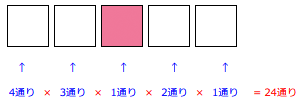
これで完成です。あとは、下に書いた○通りの○の数をすべてかければ、答えがでます。
つまり、
4×3×1×2×1＝24（通り）
が正解です。

答え：24通り

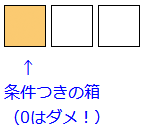
この問題も数を一列に並べて整数をつくる問題なので、これまでと同じように「ボックス法」で解くことができます。3つの数を並べるので、準備する箱は3つです。この3つの箱の中に順に1つずつ数を入れていくことを考えます。ただし、条件があります。3桁の整数をつくるので、一番左端の箱（百の位）は0が使えません。この条件のある箱から考えていきます。

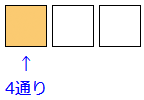
まず、一番左端の箱（百の位）は0以外の1、2、3、4のいずれか一つの数が入るので、4通りです。

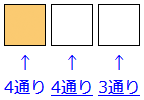
次に真中の箱（十の位）です。0、1、2、3、4の5つのうち、一番左端の箱（百の位）に1つの数を入れたので、残りは4つです。ここには0もＯＫなので、4通りの入り方があります。
同じように、一番左端の箱（一の位）には、残った3つの数のうち、どれか一つが入るので3通りです。

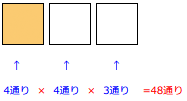
最後にかけ算をして答えを出します。
4×4×3＝48（通り）
です。

答え：48通り

この問題も並べる問題なので、これまでと同様にボックス法で解きます。ただし、「両親がとなりあう」という条件があります。「特定の箱に特定のものを入れなければならない」というこれまでの条件とは違います。どのように考えればよいのでしょうか？　両親を父と母に分けないで、ひとかたまりとして考えます。ひとかたまりで考えれば、必ずとなりあうことになりますね。
両親ひとかたまり（父・母）と子供3人（A子、B子、C子）で考えるので、4つの箱を準備します。そして、順に箱に入ってもらいます。

たとえば、

と入った場合は、 C子、父、母、A子、B子 の順に並ぶことを意味します。

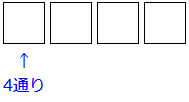
それでは、ボックス法で考えていきましょう。
まず、左端の箱から今までと同じように考えます。
両親ひとかたまりと子供3人のうち、誰かが入るので、4通りです。

そして、左から2番目の箱から順に、3通り、2通り、1通りとなります。
かけ算をして、
4×3×2×1＝24通り
となります。

ところで、両親はひとかたまりで考えました。ここでは父・母の順で考えましたが、逆の母・父の並び方もあります。ということは、並び方は、先に出した24通りの2倍になります。
たとえば、

のように並んだ場合、父と母の順が逆になって

の並び方もあるのです。最初に計算した24通りは、両親をひとかたまりと考え、父・母の順で考えましたが、逆の並び方もあるので、2倍の並び方があるのです。 結局、24×2＝48通りでこれが正解です。

答え：48通り