学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
進数法の問題
｢片手でいくつまで数えられますか？」と聞かれたら、普通は「5まで」と答えることと思います。実は、2進法を使って、器用に指を曲げたり伸ばしたりすれば、片手で31まで数えられるのです。なぜ、そんなことが可能なのかを今回は学びます。
※この分野の問題は、進数法をきちんと理解した上で考えようとすると大抵は混乱してしまいます。入試問題の中でも難問に分類されます。中学以降にきちんとした形で学びますので、最初は「●進法の問題」とは考えずにパズル感覚で問題を解きながら、理解を深めていくほうが、身につくようです。
解き方のポイント
かくれたきまりをみつける。
…実際の問題では、ます目やランプ、図形などが並べられた形で出題されることがほとんどです。それぞれの位置（それぞれの位）がいくつの数を表しているかがわかれば問題は解けたようなものです。
問題1
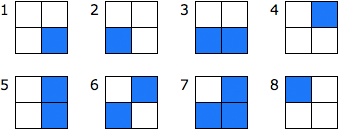
次の図のマスは、あるきまりで次のように数を表しています。
この決まりで12を表すとどのようになりますか。
（1）このきまりで12を表すとどのようになりますか。右の図に書き入れなさい。
（2）この4つのマスでは、最大いくつまで表せますか。
解法
まずは一つずつ見ていきながら、かくれたきまりをみつけましょう。
それぞれの位置のマスが表している数をまとめると、次のようになります。
ここでみつけたかくれたきまりは次の3つです。
1．ぬってあるマスが、1、2、4、8を表していること
2．それが2倍ずつ増えているということ
3．ぬってあるマスが表している数を合計すれば、全体があらわしている数になっていること
このきまりで、考えると、8以上の数も次のようにつくることができます。
＝10 
＝14 です。 12は8＋4だから 
となります。
答え：
（2）この4つのマスが、最大の数となるときは4つのマスすべてがぬってあるときだから、
1＋2＋4＋8＝15
答え：15
問題の図から 
＋ 
＝15と考えることもできます。
問題2
下のような5つランプが並んでいます。つけたり消したりして、右のように数を表します。ランプがついた状態が●で、消えた状態が○です。
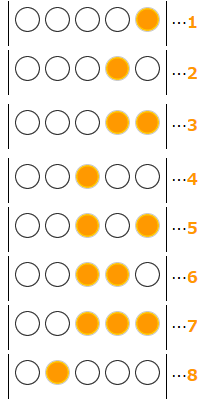
（1）エとオのみがついたときは、いくつですか。
（2）この5つのランプでは、最大いくつまで表せますか。
（3）500を表すためには何個のランプをつけ加えることが必要ですか。
解法
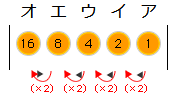
問題1と同じように一つずつ見てゆき、かくれたきまりをみつけましょう。
すると、アイウエオはそれぞれ1、2、4、8、16を表していることがわかります。
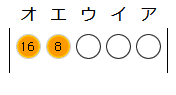
（1） エ、オのみがついたときは、8＋16＝24 です。
答え：24
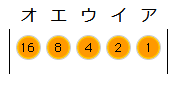
（2） この5つのランプで最大の数を表しているときは、
この5つのランプがすべてついたときだから、
1＋2＋4＋8＋16＝31となります。
答え：31
ここではランプがつく、つかないで数を表しましたが、片手で5本の指を曲げたり、伸ばしたりして、器用に使えば、31まで数えられるのです。
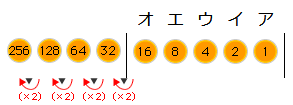
（3） ひとつずつランプをつけ加えていきます。表す数は2倍ずつ増えていきます。
3個つけ加えた時点で、
1＋2＋4＋8＋16＋32＋64＋128＝255 までを表すことができ、500にはいたりません。
4個つけ加えた時点で、
1＋2＋4＋8＋16＋32＋64＋128＋256＝511 となり、500を表すことができます。
500を表すためには、合計9個のランプが必要で、4個のランプをつけ加えることが必要です。
答え：4個
ちなみに、500を表してみると、次の通りです。
さらに5つ目のランプをつけ加えると、512を表します。ここではランプがつく、つかないで数を表しましたが、10本の指を曲げたり、伸ばしたりして、器用に使えば、なんと1023まで数えられるのです。
問題3
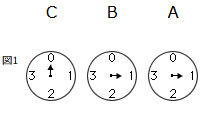
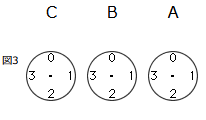
右の図のような装置にコインを1枚入れると、Aの目盛が1目盛進みます。Aが1回りすると、Bの目盛が1目盛進みます。Bが1回りするとCの目盛が1目盛進みます。コインを5枚入れると、図1のようになります。
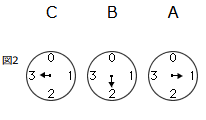
（1）はじめて図2のように針がとまったとすると、コインは何枚入れたことになりますか。
（2）コインを36枚入れると、針はどの位置に示されるか図3の中に書き入れなさい。
解法
（1）
Aはコインを1枚入れると、1目盛進むのであるから、Aの1目盛は1を表しています。
BはAが1回りしたら、1目盛進むので、Bの1目盛は4を表しています。
CはBが1回りしたら、1目盛進むので、Cの1目盛は16を表しています。
結局、A、B、Cの順に
を表していることがわかります。順に4倍になっています。
このきまりで考えると、図1は
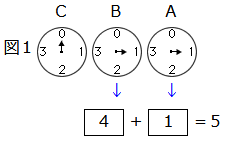
で5を表していることになります。問題文にも「コインを5枚入れた」と書いてあります。
問題1と問題2は順に2倍になっていました。2進法の問題（位どり）だからです。この問題3では、順に4倍になっています。この問題は4進法の問題（位どり）なのです。
では、図2も同じ決まりで考えてみましょう。
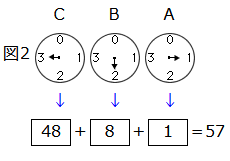
Aは1目盛が1だから1
Bは1目盛が4で、2を指しているので4×2＝8
Cは1目盛が16で3を指しているので16×3＝48
合計は、1＋8＋48＝57
答え：57枚
（2）36は16が2つ（＝32）と4が1つ（＝4）だから、
Cの目盛が2、Bの目盛が1、Aの目盛は0を指すことになります。
答え：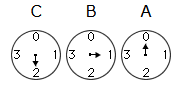 
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
