学校の危機管理
世界の教育事情
科学夜話
今どきの小学生
魔方陣（まほうじん）
今回は「魔方陣（まほうじん）」です。たて・よこ・ななめ、どの線に沿って足してもその合計が同じような方陣のことを言います。魔方陣はパズル的な要素が強く、挑戦しているうちに計算が理解でき、計算力も自然に高めることができるので、計算が苦手な子にとって、とてもよい教材になります。勘でもある程度解くことはできますが、ここでは考え方で解く方法を説明します。
ポイントは次の通りです。
ポイント1）数が限定されるところから順に考える（おのずと決まってくるところから考える）。
ポイント2）組み合わせで考える（組み合わせの少ないところから考える）。
問題1
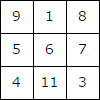
右の図1で、たて・横・ななめに並んでいる3つの数の和は次のようにすべて等しく18になります。
| たて | 9＋5＋4 | 1＋6＋11 | 8＋7＋3 |
| 横 | 9＋1＋8 | 5＋6＋7 | 4＋11＋3 |
| ななめ | 9＋6＋3 | 8＋6＋4 |
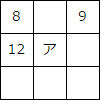
このような図を「魔方陣」といいます。図1と同じように、図2の魔方陣をつくろうと思います。これについて次の問いに答えなさい。
（1）図2の8と12の和と、9とアの関係からアに入る数を求めなさい。
（2）この魔方陣に使われている9個の数の中で、一番大きな数を求めなさい。
解法
（1）正解から先に言ってしまうと、アに入る数は11です。
この魔方陣では、8＋12（＝20）と9＋アが等しくなるからです。その理由はわかりますか？
下の図2-・で、8＋12＋イと9＋ア＋イが同じになるから、共通にたしているイを引いて考えても、両者は等しくなるからです。
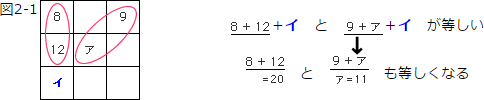
9＋ア＝20 より、ア＝11
答え
ア＝11
図1で同じ箇所を見ても、確かにたした数は等しくなっています。
このように、数を組み合わせて考えていくことが、魔方陣の問題を解く上でのポイントになります。
（2）それでは、順にこの魔方陣を完成させていきましょう。ポイントは次の通りです。
ポイント1）数が限定されるところから順に考える（おのずと決まってくるところから考える）。
ポイント2）組み合わせで考える（組み合わせの少ないところから考える）。
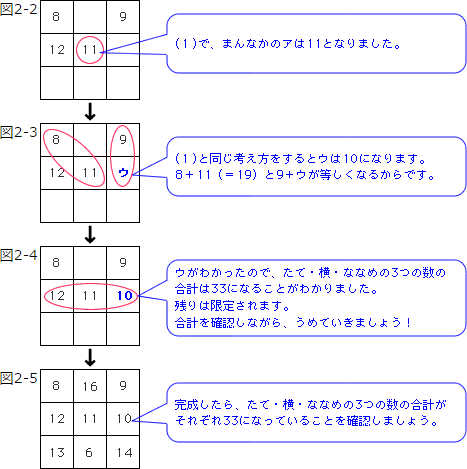
ここでは、魔方陣に使われている9個の数の中で、一番大きな数を求めることが問題でした。
正解は16です。
答え
16
問題2
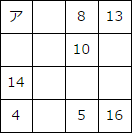
右のようなます目に、1から16までの数字のうち、使っていない数字を1つずつ入れて、たて・横・対角線の数字の合計が等しくなるようにします。アに入る数字を求めなさい。
解法
たて・横・対角線それぞれ1列の4つの数の合計はいくつでしょうか？それがわかれば、数が限定されて、すぐにうまりそうなます目がいくつかありそうです。
1から16までの数字を1つずつ入れていくわけですから、1から16までの16個の数字の合計を計算して、4等分すれば（4で割れば）、たて・横・対角線それぞれの数の合計が出ます。
そこで、1から16までの16個の数の合計を計算しますが、「数列」のところで説明したガウス少年の方法で次のように計算します。
たて・横・対角線それぞれ1列の4つの数の合計は、34ということがわかりました。
それでは、数が限定されるところから順に考えていきましょう。
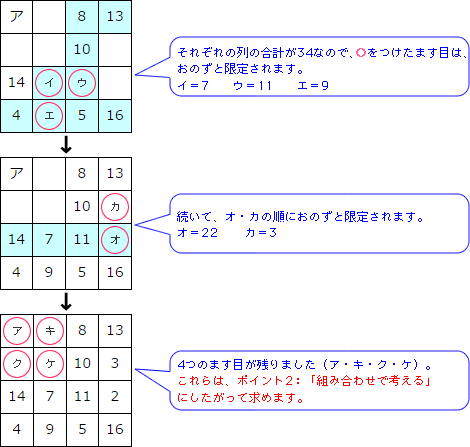
これまでで使われていないのは、1、6、12、15の4つです。つじつまが合うように考えながら求めていきます。問題1で説明しましたが、左下の図で色をつけたます目の部分の合計は3つとも等しくならなければなりません。
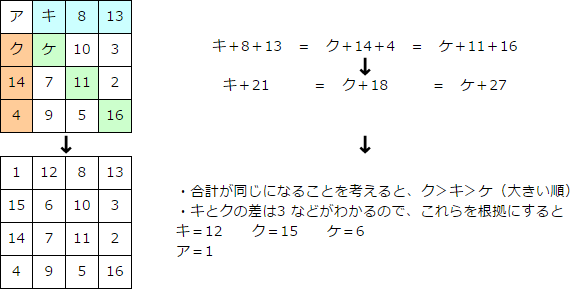
答え
ア＝1
問題3
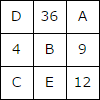
右の図のたて・横・ななめの3個の整数をかけた積は、みな等しくなっています。Bの数はなんですか？
ただし、0は使わず、同じ数は2度以上使いません。
解法
最後の問題はたて・横・ななめの数をたすのではなく、かける魔方陣です。考え方のポイントは同じです。数の組み合わせで考えて、数が限定されるところから、うめていきましょう。
まず、中央の十字に注目してみます。
A×Bが12に限定されたということは、AとBの組み合わせは、
（1，12）（2，6）（3，4）のいずれかの組み合わせになります。
このうち、（1，12）（3，4）の組み合わせは、すでに使われている数なので、（2，6）の組み合わせがA，Bに入ることになります。
実際にあてはめてみます。
A＝2、B＝6があてはまっています。
他のたて・横・ななめの3つの数の積が216になるように決めるとC＝18となります。
実際に、C＝18をあてはめて、すべてのたて・横・ななめの3つの数の積を計算してみると、やはり216になっています。Bを求めることが問題でしたのでB＝6が正解です。
答え
B＝6
教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは，もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
