倍数・公倍数・最小公倍数

たて3cm、横5cmの長方形の紙を同じ向きにすきまなく並べて、できるだけ小さな正方形を作るとき、正方形の１辺の長さは何cmになりますか。また、何枚の長方形の紙が必要ですか。
解法を見る


A町行きのバスは8分おき、B町行きのバスは12分おき、C町行きのバスは18分おきに出発します。午前8時に3台のバスが同時に発車しました。次に3台のバスが同時に出発するのは何時何分ですか。
解法を見る


２つの分数とのそれぞれに同じ分数をかけたらどちらも整数になりました。かける分数の中で最も小さいものを求めなさい。
解法を見る

---

たて3cm、横5cmの長方形の紙を同じ向きにすきまなく並べて、できるだけ小さな正方形を作るとき、正方形の１辺の長さは何cmになりますか。また、何枚の長方形の紙が必要ですか。

■ 解法
この問題は、3と5の最小公倍数が計算できれば、答えが出ますが、最小公倍数の知識を使う理由を理解しておくことが大切です。
次のように具体的に並べて考えてみましょう。

【1枚のとき】



【2枚を並べたとき】
　　


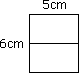
【3枚を並べたとき】
　　


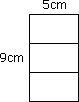
【4枚を並べたとき】
　




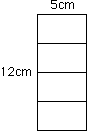
上の例では、どれも正方形にはなっていませんが、たての長さと横の長さになりうる数は次の通りであることが、理解できると思います。

たての長さになりうるのは、
3cm、6cm、9cm、12cm、15cm、18cm、21cm、24cm、27cm、30cm・・・つまり3の倍数です。

横の長さになりうるのは、
5cm、10cm、15cm、20cm、25cm、30cm、35cm、40cm、45cm、50cm・・・つまり5の倍数です。

正方形になるのは、たてと横の長さが一致したときなので、今書き出した中では15cm、30cmとなります。
つまり、3の倍数と5の倍数とで、共通な倍数（＝公倍数）が正方形の一辺の長さになるわけです。
問題では、できるだけ小さな正方形を作るという条件なので、1辺の長さは、公倍数の中で一番小さな数（最小公倍数）の15となり、１辺が15cmの正方形が正解です。
このとき使う長方形の紙はたて5枚（15÷3を計算）、横3枚（15÷5を計算）となります。つまり合計15枚（5×3を計算）です。

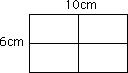
【正解の図】


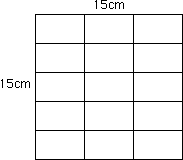
■ 答え：1辺の長さが15cm、合計15枚が必要

---

A町行きのバスは8分おき、B町行きのバスは12分おき、C町行きのバスは18分おきに出発します。午前8時に3台のバスが同時に発車しました。次に3台のバスが同時に出発するのは何時何分ですか。

■ 解法
これも8と12と18の最小公倍数を求めて答えを導き出す問題です。計算して答えを出すことは比較的簡単ですが、なぜ、最小公倍数の知識が使えるのかを理解することが大切です。
そのためには、まずは、次のように具体的に書き出して考えましょう。

A町行きのバスは8分おきなので、発車時刻は、
8：00　8：08　8：16　8：24　8：32・・・となります。

B町行きのバスは12分おきなので、発車時刻は、
8：00　8：12　8：24　8：36　8：48・・・となります。

C町行きのバスは18分おきなので、発車時刻は、
8：00　8：18　8：36　8：54　9：12・・・となります。

この問題では、同時に発車する時刻を求めますが、このように時刻表を作っているとちょっと大変そうです。そこで、この時刻表を次のように8時ちょうどから計って、それぞれのバスが何分後に発車するのかを考えます。

A町行きのバスは8分おきなので、
8分後　16分後　24分後　32分後　40分後・・・となります（8の倍数）。

B町行きのバスは12分おきなので、
12分後　24分後　36分後　48分後　60分後・・・となります（12の倍数）。

C町行きのバスは18分おきなので、
18分後　36分後　54分後　72分後　90分後・・・となります（18の倍数）。

つまり、共通に発車するのは何分後かを求め、時刻を求めればよいわけです。
それを求めるためには、８と１２と１８の倍数の中で共通な数。つまり公倍数を求めればよいわけです。問題では、「次に3台のバスが同時に出発するのは何時何分ですか。」ということなので、公倍数の中で一番小さい数、つまり最小公倍数を求めればよいことになります。
最小公倍数を連除法で求めてみます。

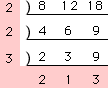
最小公倍数は、2×2×3×2×1×3＝72　なので、8時から数えて72分後が「次に3台のバスが同時に出発する時刻」です。
つまり、8時00分＋72分＝9時12分　でこれが正解です。

■ 答え：9時12分

---

２つの分数とのそれぞれに同じ分数をかけたらどちらも整数になりました。かける分数の中で最も小さいものを求めなさい。

■ 解法
この問題も難しそうですが、考え方を理解して、解き方を覚えてしまえば、すぐに解けてしまいます。
まずはから考えてみましょう。かける分数をとして、かけた結果、整数になる条件（分母を１にするための条件）考えます。

×

【具体的な例】







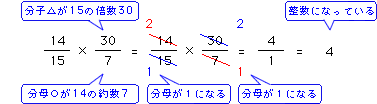
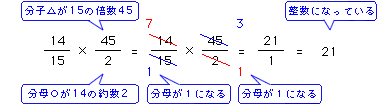
上の説明より、かける分数の分母○は14の約数、かける分数の分子△は15の倍数でなければならないことがわかりましたか？
同じようにについても考えると、かける分数の分母○は35の約数、かける分数の分子△は24の倍数でなければならないことがわかります。

問題では、この２つの分数に、ある分数をかけたら、どちらも整数になったということなので、かける分数の分母は14と35の公約数、かける分数の分子は15と24の公倍数であれば、両方のかけ算の結果が整数になるはずです。
さらに、この問題では「かける分数は最も小さいもの」ということなので、分母は一番大きく（最大公約数）、分子は一番小さいもの（最小公倍数）を選ぶ必要があります。まとめると、次の通りです。

かける分数の分母・・・14と35の最大公約数＝７
　

かける分数の分子・・・15と24の最小公倍数＝120（3×5×8）
　

よって、求める分数（かける分数）はまたはとなります。


■ 答え：または