2003.02.11
仕事算
仕事算とは、ある仕事(ペンキを塗る、水そうに水を入れるなど)をするときの仕事の速さやかかる時間などを求める計算です。仕事算の問題では、仕事の全体の量は問題文中に書かれていません。そのため、普通は仕事の全体の量を仮に1と決めて解きます。この解き方は、多くの教科書や参考書に載っているので、今回は別の方法をご紹介します。
ある建物の壁のペンキを塗り替えるとき、Aの人が1人で塗ると2時間かかり、Bの人が1人で塗ると3時間かかるそうです。
(1)Aの人は1時間あたり、全体に対してどのくらいの仕事をする(ペンキを塗る)ことができますか。
(2)2人が一緒に仕事をはじめた場合、何時間何分で塗り終えることができますか。
解法を見る
水そうに水をいっぱい入れるのに、太い管1本では12分かかり、細い管1本では16分かかります。今、太い管2本と細い管4本をいっしょに使って水を入れると、何分何秒でいっぱいになりますか。
解法を見る
ある仕事をするのに、A君1人では9日間かかり、B君1人では、15日間かかります。この仕事をA君が6日間行ったあと、残りをB君が行います。この場合、この仕事を終わらせるためには何日間必要ですか。
解法を見る
1:仕事全体の量を決定する。
2:それぞれの担当者が単位時間にできる仕事の量を求める。
3:二人の担当者が一緒に仕事をしたときに単位時間にできる仕事の量を求める。
4:仕事全体の量を二人の担当者が一緒に仕事をしたときにかかる時間を求める。
※単位時間とは、1秒間、1分間、1時間、1日間、1年間…などのことです
ある建物の壁のペンキを塗り替えるとき、Aの人が1人で塗ると2時間かかり、Bの人が1人で塗ると3時間かかるそうです。
(1)Aの人は1時間あたり、全体に対してどのくらいの仕事をする(ペンキを塗る)ことができますか。
(2)2人が一緒に仕事をはじめた場合、何時間何分で塗り終えることができますか。
■ 解法
仕事算では、この問題のように、しなければならない仕事の全体の量(ここでは壁の面積)がどれだけあるのかが具体的に書かれていません。そのため、仕事の全体の量は問題を解く本人が、自由に決めていいわけです。つまり、5でも120でも1000でも自由に決めていいということです。そこで、ふつうの解き方では、仕事の全体の量を1と仮に決めて解きますが、ここではさらに計算を楽にするために、次のような決め方をします。
ここでは、2と3の公倍数になるので、6、12、24・・・などです。どれでもよいのですが、最小公倍数が問題を解く上で一番計算しやすいので、6を選びます。
(1)全体の仕事の量を6(壁の面積)と決めました。
この6の面積の壁にペンキを塗るのにAの人は2時間かかるので、1時間あたりでは3の面積にペンキを塗る(仕事をする)ことになります( 6 ÷ 2 = 3 )。これは全体6に対して3なので、
■ 答え:
※Aの人が1人で塗ると2時間かかるので、あるから1時間あたりでは半分の2分の1という考え方でもOKです
(2)(1)と同じようにBの人が全体に対して1時間あたりどのくらいの仕事をするのかを求めてみます。
6の面積の壁に壁のペンキを塗るのにBの人は3時間かかるので、1時間あたりでは2の面積にペンキを塗る(仕事をする)ことになります。
ここで、AとBが一緒に仕事をすると、
(Aの1時間あたりの仕事量)+(Bの1時間あたりの仕事量)= 3 + 2 = 5
つまり、AとBが一緒に仕事をすると、1時間あたり5の面積にペンキを塗ることができます。
すべて、ペンキを塗り終えるには、全体の面積が6なので、
6 ÷ 5 =
■ 答え:1時間12分
※面積(仕事の量)に単位を付けないで考えてきましたが、説明するときには、仮に6〔m2〕等の単位(何でもよい)を付けて考えると具体的になってわかりやすくなると思います。
水そうに水をいっぱい入れるのに、太い管1本では12分かかり、細い管1本では16分かかります。今、太い管2本と細い管4本をいっしょに使って水を入れると、何分何秒でいっぱいになりますか。
■ 解法
ここでも、仕事の全体の量(ここでは水そうの容積)が書かれていません。そこで、問題1と同じように、かかる時間の公倍数で仕事の全体の量を決めましょう。
仕事の全体の量(水そうの容積)=12と16の公倍数=48、96、144・・・(最小公倍数の倍数が公倍数)
ここでも最小公倍数の48を全体の仕事量(水そうの容積)とします。 (※96でも144でも別の数でも答えはみんな同じになります。)
【連除法による最小公倍数 の求め方】
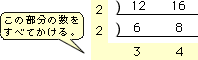
全体の仕事の量(水そうの容積)を48に決めました。ここで、太い管と細い管の1分あたりの仕事量を求めて見ましょう。
48の容積の水そうに水をいっぱいに入れるためには、
太い管は12分かかるので、1分あたり4の水を入れることになります( 48 ÷ 12 = 4 )。
細い管は16分かかるので、1分あたり3の水を入れることになります( 48 ÷ 16 = 3 )。
ここで太い管2本と細い管4本をいっしょに使って水を入れると、
(太い管2本分の1分あたりの仕事)+(細い管4本分の1分あたりの仕事)
=( 4 × 2 )+( 3 × 4 )
=8 +12
=20
つまり、1分あたり20の水を入れることができるわけです。
全体は48なので、水そうの水をいっぱいにするためにかかる時間は
48 ÷ 20 =
■ 答え:2分24秒
※体積(仕事の量)に単位を付けないで考えてきましたが、説明するときには、仮に6〔リットル〕等の単位(何でもよい)を付けて考えると具体的になってわかりやすくなると思います。
ある仕事をするのに、A君1人では9日間かかり、B君1人では、15日間かかります。この仕事をA君が6日間行ったあと、残りをB君が行います。この場合、この仕事を終わらせるためには何日間必要ですか。
■ 解法
これまでと同じように、かかる時間の公倍数で仕事の全体の量を決めましょう。
仕事の全体の量=9と15の公倍数=45、90、135・・・(最小公倍数の倍数が公倍数)
ここでも最小公倍数の45を全体の仕事量とします。(※90でも135でも別の数でも答えはみんな同じになります。)
【連除法による最小公倍数 の求め方】
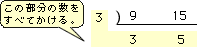
全体の仕事の量を45に決めました。ここで、A君とB君の1日あたりの仕事量を求めてみましょう。
45の仕事を終わらせるためには、
A君は9日間かかるので、1日あたり5の仕事をすることになります( 45 ÷ 9 = 5 )。
B君は15日間かかるので、1日あたり3の仕事をすることになります( 45 ÷ 15 = 3 )。
まず、A君が1人で1日あたり5の仕事をして、6日間働くので、全体45のうち30の仕事を終わらせます( 5 × 6日間 = 30 )
残りの仕事の量は15です( 45 - 30 = 15 )。
この15をB君は引き受けるわけですが、B君は1日あたり3の仕事をするので、5日間かかります。( 15 ÷ 3 = 5 )。
よって、合計で11日間かかります( 6 + 5 = 11 )。
■ 答え:11日間
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
