数列（等差数列）

１から１００までの数（整数）全部たすといくつになりますか。
解法を見る


ある規則にしたがって数を次のように並べました。
２，５，８，１１，１４　・・・・・・・
（１）１２番目の数はいくつですか。
（２）６２は何番目の数ですか。
（３）はじめから１０番目までの数をすべてたすといくつになりますか。
解法を見る


０,０，４,４，８,８，１２,１２，・・・・・・・のように数を順に２つずつ並べた数列があります。
（１）２０番目の数はいくつですか。
（２）最初の数から１００番目までの数をすべてたすといくつになりますか。
解法を見る

---

１から１００までの数（整数）全部たすといくつになりますか。

■ 解法
「１から１００までの数（整数）全部たすといくつになりますか？」これは、数学者のガウスが少年のころ先生から出されて、あっという間に解いてしまい、みんなを驚かせたそうです。この問題をガウス少年は次のように解きました。

１から１００を順に書き、その下に１００から１までを逆に並べて上下をたします。

	1	2	3	4	5	･･･	98	99	100
+）	100	99	98	97	96	･･･	3	2	1
	101	101	101	101	101	･･･	101	101	101

すると、すべて１０１にきれいにそろいました。１０１が１００個できたので、１０１を１００回たすと
１０１×１００＝１０１００になります。ところが、これは、はじめから１００までの数をすべてたしたものの２倍になっているので、半分にして１０１００÷２＝５０５０が正解です。

ここで忘れてはならないことは、上下に並べてたし算をすると、数がそろって大変便利ですが、計算結果は求める和の2倍になって出てくるので、最後に必ず２で割るということです。


■ 答え：５０５０

---

ある規則にしたがって数を次のように並べました。
２，５，８，１１，１４　・・・・・・・
（１）１２番目の数はいくつですか。
（２）６２は何番目の数ですか。
（３）はじめから１０番目までの数をすべてたすといくつになりますか。

■ 解法
（１）この数列の規則は３ずつ増えているということです。



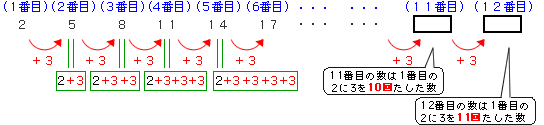
１番目は最初の数で　　　　　２
２番目は２に３を１回たして、２＋３
３番目は２に３を２回たして、２＋３＋３
４番目は２に３を３回たして、２＋３＋３＋３
５番目は２に３を４回たして、２＋３＋３＋３＋３

ここで、もう一つの大切な規則があります。それは、２番目の数は最初の数２に３を１回たした数、３番目の数は３を２回たした数、４番目の数は３を３回たした数、・・・となっています。
つまり、□番目の数は□より１少ない回数分３をたすことになります。このように考えると、１２番目の数は１番目の２に３を11回たした数になります。発展させて１００番目の数は２に３を９９回たした数になります。

１２番目の数は、	２＋３＋３＋３＋・・・＋３ (３を１１回たす）
	＝２＋３×１１
	＝２＋３３
	＝３５

■ 答え：３５


■ 解法
（２）６２は最初の数の２に６０をたした数です。
　　　６０は３を２０回たしたものなので、６２は２１番目の数です。

２＋３＋３＋３＋・・・＋３　＝６２ (３を２０回たす）

２０回たしたということは、６２は２１番目

■ 答え：２１番目

□番目の数は□より１少ない回数分３をたす。つまり、６番目の数を求めたいときは、最初の２に３を５回たして求めることになります。これは、数を並べたときの数と数のすき間の数になります。ちょうど植木算で説明した木の本数と区画の数の関係と同じです。

1番目	2番目	3番目	4番目	5番目	6番目
２	５	８	11	14	17

公式にすると、
（□番目の数）＝（最初の数）＋（差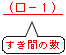）×となります。




■ 解法
（３）これも問題１のガウスの方法で計算できます。まず、10番目まで書き出してみます。

これを全部そのままたすのでは、ちょっと大変そうです。そこで、つぎのように、上に書いた数の下に逆の順番で書き並べて上下をたしてみましょう。


　すると、すべて３１にきれいにそろいました。３１が１０個できたので、３１を１０回たすと
３１×１０＝３１０になります。ところが、これは、はじめから１０番目までの数をすべてたしたものの２倍になっているので、半分にして３１０÷２＝１５５が正解です。

（３）を式でまとめると、
（２＋２９）×１０÷２＝１５５　となります。
公式にすると、
（最初の数＋最後の数）×（個数）÷２　となります。

■ 答え：１５５

---

０,０，４,４，８,８，１２,１２，・・・・・・・のように数を順に２つずつ並べた数列があります。
（１）２０番目の数はいくつですか。
（２）最初の数から１００番目までの数をすべてたすといくつになりますか。

■ 解法
（１）この数列の規則は、２つずつ組になって４ずつ増えています。このように組になっている数列は組にして考えます。

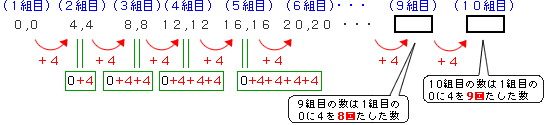
１組目は、１番目と２番目の数 ２組目は、３番目と４番目の数 ３組目は、５番目と６番目の数 ４組目は、７番目と８番目の数　 　　　　　　… ９組目は、１７番目と１８番目の数 １０組目は、１９番目と２０番目の数　 　　　　　　… ５０組目は、９９番目と１００番目の数

緑色の文字に着目すると、2倍になっているので、わかりやすいと思います。

のように組がつくられているので、２０番目の数は１０組目に含まれることがわかります。１０組目の数は１組目の０に４を９回たした数なので、
（１０組目の数）＝（１９番目と２０番目の数）＝０＋４×９＝３６
となります。


■ 答え：３６

■ 解法
（２）まず、１００番目の数は、５０組目に含まれることがわかります。これまでと同様に数を並べて考えましょう。



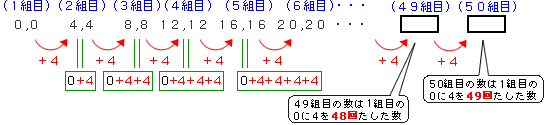
５０組目の数は１組目の０に４を４９回たした数なので、
（５０組目の数）＝０＋４×４９＝１９６

ここでも，ガウスの方法ですべてたしてみます。

	1組目	2組目	3組目	･･･	48組目	49組目	50組目
	0,0	4,4	8,8	…	188,188	192,192	196,196
	50組目	49組目	48組目	･･･	3組目	2組目	1組目
+)	196,196	192,192	188,188	･･･	8,8	4,4	0,0
	196,196	196,196	196,196	･･･	196,196	196,196	196,196

すべて１９６にきれいにそろいました。１９６がここでは１００個できたので、１９６を１００回たすと
１９６×１００＝１９６００になります。
ところが、これはすべてたしたものの２倍になっているので、１９６００÷２＝９８００

■ 答え：９８００
数列の和の公式で計算すると、公式は
（最初の数＋最後の数）×（個数）÷２なので、
最初の数＝０，最後の数＝１９６，個数＝５０(組）
（０＋１９６）×５０÷２＝１９６×５０÷２＝９８００÷２
＝４９００
それそれの組には同じ数が２つずつふくまれるので、すべてたした場合はこの２倍になる。
４９００×２＝９８００