おすすめ特集記事

算数の教え上手

2002.12.10
  • twitter
  • facebook
  • はてなブックマーク
  • 印刷

虫食い算

虫食い算とは、下の問題のように、式の中に□があり、あてはまる数を求める計算です。今回は、簡単な式と比べて解く方法で説明します。実際の入試問題などでは、分数や小数が含まれた形で出題されることが多いのですが、今回説明する方法と同じ方法で解くことができます。


次の□にあてはまる数を求めなさい。
(1)　3＋□＝5　　(2)　□＋1＝3　　(3)　3－□＝2
(4)　□－2＝3　　(5)　3×□＝6　　(6)　□×2＝6
(7)　6÷□＝2　　(8)　 □÷2＝3
解法を見る


次の□にあてはまる数を求めなさい。
（1） □＋25＝149　　（2） 569－□＝21
（3） 12×□＝108　　（4） □÷16＝3
解法を見る


次の□にあてはまる数を求めなさい。
（1） 2＋7＋□＝15　　（2） 4×3×□＝60
（3） □－56÷7＝18　　（4） □÷（5＋3）＝16
解法を見る


次の□にあてはまる数を求めなさい。
（1） □÷12×5＝20
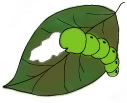
（2） 225÷（□－15）＝75
解法を見る

（今回の卒業問題）
7×□÷16＋24＝80の□にあてはまる数を求めなさい。
解法を見る


次の□にあてはまる数を求めなさい。
(1)　3＋□＝5　　(2)　□＋1＝3　　(3)　3－□＝2
(4)　□－2＝3　　(5)　3×□＝6　　(6)　□×2＝6
(7)　6÷□＝2　　(8)　 □÷2＝3

■ 解法
これらは、虫食い算の基本問題です。暗算ですぐに答えが出ると思います。ただし、頭の中で自分は何を計算したのかを知ることが大切です。

問　題 答　え
（1） 3＋□＝5 □＝2
（5－3を計算した）
（2） □＋1＝3 □＝2
（3－1を計算した）
（3） 3－□＝2 □＝1
（3－2を計算した）
（4） □－2＝3 □＝5
（3＋2を計算した）
（5） 3×□＝6 □＝2
（6÷3を計算した）
（6） □×2＝6 □＝3
（6÷2を計算した）
（7） 6÷□＝2 □＝3
（6÷2を計算した）
（8） □÷2＝3 □＝6
（2×3を計算した）

準備体操の問題は、暗算が可能で、視覚的で解いてしまった方も多いと思いますが、次は数が大きめの虫食い算を解いてみましょう。

次の□にあてはまる数を求めなさい。
（1） □＋25＝149　　（2） 569－□＝21
（3） 12×□＝108　　（4） □÷16＝3

■ 解法
次のように、暗算ができる簡単な式をつくって、比べて解きます。

（1）　□＋25＝149について、2＋3＝5で考えてみます。もちろん、他の足し算の式でもＯＫです。
すると、2の部分が□、3が25、5が14９に対応します。2は5－3だから、問題の□は149－25で、124が正解です。



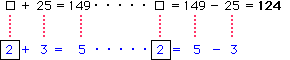
（1）と同じ方法で他の問題も考えてみましょう。青文字で示した簡単な式と比べて考えます。

（2）　　


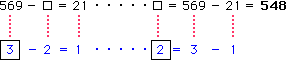
（3）　　


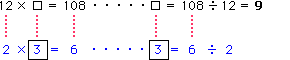
（4）　　

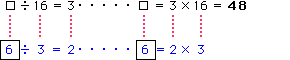
■ 答え：（1） 124　（2） 548　（3） 9　（4） 48

虫食い算の解法1：簡単な式を作って、比べて解く。

次の□にあてはまる数を求めなさい。
（1） 2＋7＋□＝15　　（2） 4×3×□＝60
（3） □－56÷7＝18　　（4） □÷（5＋3）＝16

■ 解法
虫食い算では、まず先に計算できるところがあったら先に計算して、外見をシンプルにします。シンプルになったら、問題1と同じ方法で解きます。

問題 先に計算
できる所		 簡単な式
にして計算		 答え
2＋7＋□＝15 9＋□＝15 □＝15－9 　□＝6
4×3×□＝60 12×□＝60 □＝60÷12 　□＝5
□－56÷7＝18 □－8＝18 □＝18＋8 　□＝26
□÷(5＋3)＝16 □÷8＝16 □＝16×8

　□＝128

虫食い算の解法２：先に計算できるところは計算してシンプルにする。
ここで、問題2 で登場した＝の左側の式（左辺）の計算順序を確認しておきます。
（1） 2＋7＋□
まず、2＋7　を計算してから、□を足す。
（2） 4×3×□
まず、4×3　を計算してから、□をかける。
（3） □－56÷7
まず、56÷7　を計算して、その結果を□から引く。
（4） □÷（5＋3）
まず、5＋3　を計算して、その結果で□を割る。
＝の左側の式を「左辺」といいます。
■ 答え：（1） 6　（2） 5　（3） 26　（4） 128

次の□にあてはまる数を求めなさい。
（1） □÷12×5＝20
（2） 225÷（□－15）＝75

■ 解法
（1） □÷12×5＝20で、12×5を先に計算して、□÷60＝20とシンプルにするのは、間違いです。割り算と掛け算が含まれる式では、左から順に計算することがルールだからです。つまり、この式では、□÷12を先に計算しなければならないのです。（この式の左辺の計算順序は、まず□÷12を計算してから、5をかける）

ところが、□÷12は□の正体がわからない限りは計算できません。
このように、先に計算しなければならない箇所に□が含まれる虫食い算では、先に計算しなければならない箇所を大きなに変身させます。

　 ×5＝20
↑大きなに変身
すると ×5＝20
という問題に変わりました。これまでと同様に解くと、
　 ＝4
となります。
ところで、大きなの正体は、□÷12でした。変身前に戻すと、
　 □÷12＝4
となります。これも、これまでと同じように解くと、
　

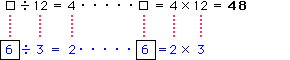■ 答え：□ = 48


（2） 225÷（□－15）＝75では、（　）を優先して、（□－15）を先に計算しなければなりません。
ところが、□－15は□の正体がわからない限りは計算できません。
（この式の左辺の計算順序は、まず□－15を計算してから、その結果で225を割る）
そこで、（1） と同じように、（□－15）を大きなに変身させます。

　 225÷＝75
↑大きなに変身
すると 225÷＝75
という問題に変わりました。これまでと同様に解くと、
　 225÷＝75
6÷＝2　⇒　　＝6÷2
　 ＝225÷75＝3
となります。
ところで、大きなの正体は、□－15でした。変身前に戻すと、
　 □－15＝3
－2＝１　　⇒　　＝2＋1
これも、これまでと同じように解くと、□＝15＋3＝18となります。

■ 答え：□ = 18

虫食い算の解法：3
先に計算しなければならない箇所に□が含まれる虫食い算では、先に計算しなければならない箇所を大きなに置き換える。
※□÷8×2のような場合は□÷16にはならないので注意


（今回の卒業問題）
7×□÷16＋24＝80の□にあてはまる数を求めなさい。

■ 解法

7×□÷16＋24＝80で先に計算しなければならない箇所は7×□なので、ここを、大きなに置き換えます。（この式の左辺の計算順序は、まず7×□を計算してから、16で割り、最後に24を足す）
÷16＋24＝80
すると、 ÷16＋24＝80
のようになりますが、これまでとは違って＝の左側に計算記号が２つ（÷と＋）あり、しかも、16＋24は計算のルール上、先に計算できないので、うまく解けそうもありません。そこで、その次に計算しなければならない÷16まで含めたさらにジャンボなに置き換えます。
＋24＝80
すると、 ＋24＝80
となり、今まで解いてきた虫食い算と同じになりました。
＋24＝80
　＋3＝5　　⇒　　＝5－3
＝80－24＝56
ここで、ジャンボなの正体は、7×□÷16だったので、
＝56
7×□÷16　＝56
ということになります。この式では、7×□を先に計算しなければならないので、ここを大きなに置き換えると、（この式の左辺の計算順序は、まず7×□を計算してから、16で割る）
÷16＝56
÷3＝2　⇒　＝2×3
＝56×16＝896
大きなの正体は7×□だったので、もとに戻すと、
7×□＝896
2×＝6　⇒　＝6÷2
□＝896÷7＝128

■ 答え： 128
おすすめの記事

この記事に関連するおススメ記事

i

「おすすめ特集記事」の最新記事

pagetop