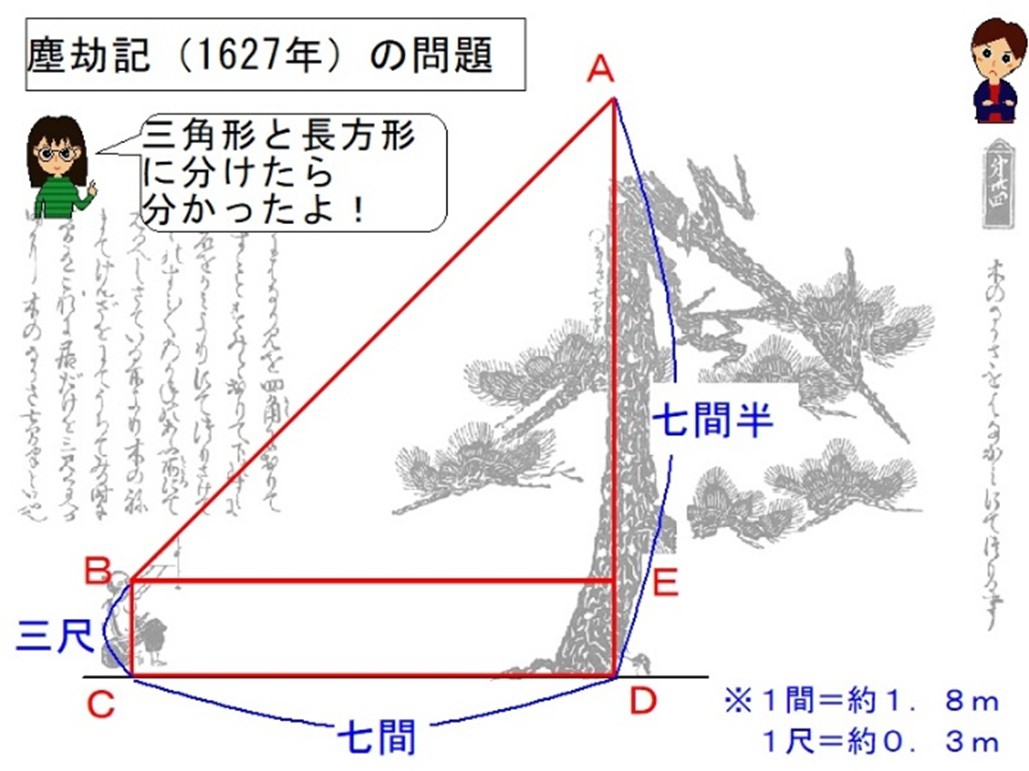
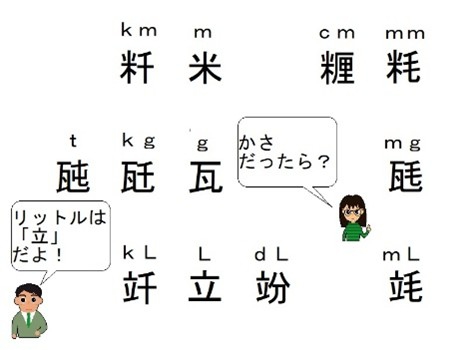
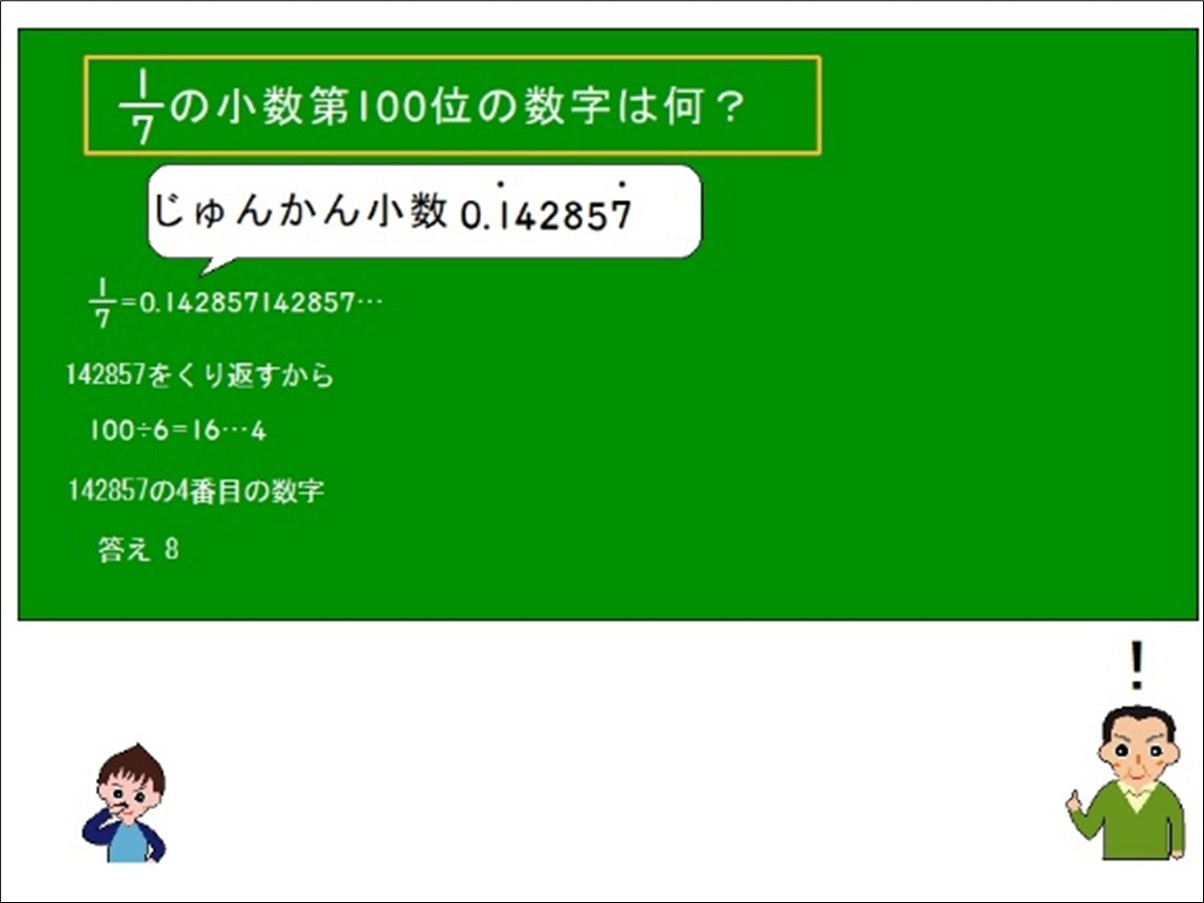
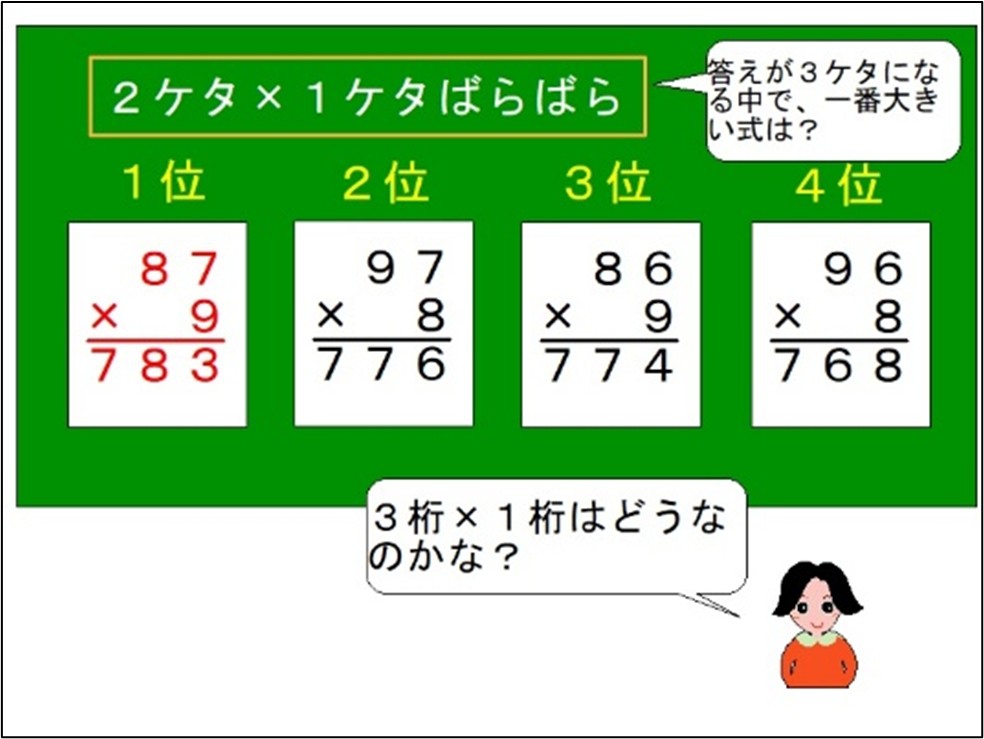
イメージが苦手でも解ける!立方体の展開図

立方体の展開図は小学校で習い、その後入学試験や資格試験など多くの場面で登場します。問題を解くためには立方体を開いて展開図にしたり、展開図を組み立てて立方体に戻したりと、頭の中でイメージする必要があります。苦手な人にとっては、とても難しいと思います。そこで今回はイメージが苦手な人でも立方体の展開図の問題を効率よく解く方法をご説明します。
問題1
次の展開図のうち立方体をつくれないものをすべて選びなさい。
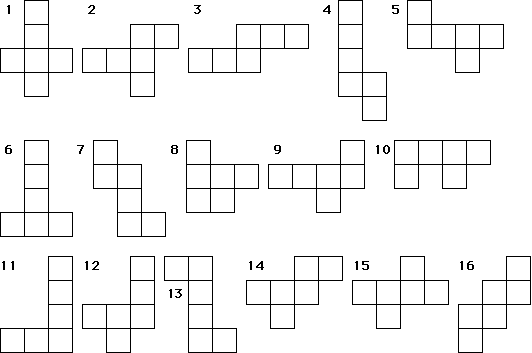
解法
ポイント①:ハンマー型が基本形
まず、立方体の展開図の基本形を覚えてください。基本形はいくつかありますが、次のハンマー型1つを覚えるとよいでしょう。
【立方体の展開図の基本形】
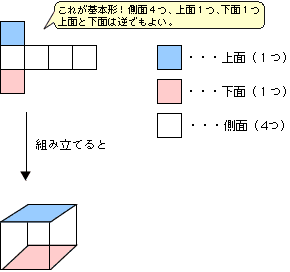
ポイント②:上面と下面を左右に好きなだけスライドさせても基本形です。
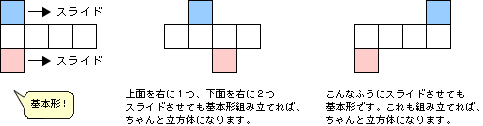
ポイント③:立方体の好きな場所(1辺)で切り離してから90°回転させて他の辺にくっつけても立方体の展開図になります。
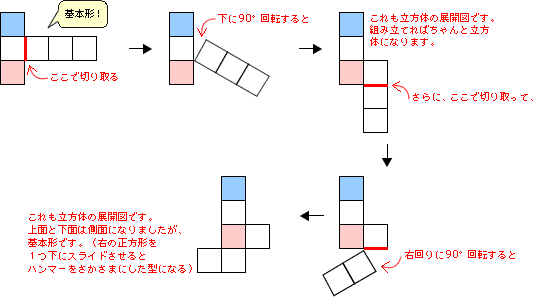
※ポイント②も結局は、上面や底面の正方形を切り離して90°回転させていることになるので、結局は、ポイント③と同じことになります。
※展開図を立方体に組み立てたとき、くっつく正方形の辺は90°回転させた先の正方形の辺であるため、この方法が使えるわけです。
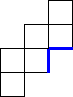
例えば、これも立方体の展開図ですが、組み立てると青線の辺がくっつきます。
それでは、問題の図をみてみましょう。 まず、ポイント①とポイント②を活用して、基本形をみつけてみましょう。次の6つはすべて基本形です。逆になったり、横になったり、縦になったりしていますが、よく見てくださいね。

※これらはすべて、側面 が4つ、上面
が4つ、上面 が1つ、下面
が1つ、下面 1つがすぐにわかる基本形です。もちろん、上面と下面は逆でもOKです。
1つがすぐにわかる基本形です。もちろん、上面と下面は逆でもOKです。
それでは、ポイント③を活用して、他もみてみましょう。![]() は切り取る線です。
は切り取る線です。
・2 について
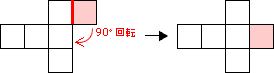
基本形
・3 について
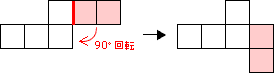
基本形
・16 について
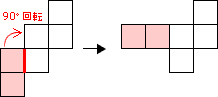
基本形
・8 について (立方体の展開図にならない例)
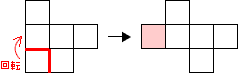
確かに基本形ですが、180°回転なので、ルール違反です。もとの 8 の図は立方体の展開図になりません。切り取って回転するのは、必ず90°でなければなりません。
以上のように考えていくと、立方体をつくれない展開図は、4、8、10、11、12の5つです。
答え 4、8、10、11、12
問題2
次の展開図で立方体を作ったとき、次の問いに答えなさい。(A~Fは面、ア~セが点)
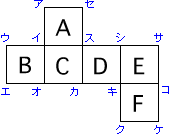
(1)エから最も遠い頂点
(2)エと重なる点
(3)オと重なる点
(4)Aと平行になる面
(5)辺ケコとつなぎあわさる辺
解法
この問題も頭の中で立方体がイメージできれば、解ける問題ですが、イメージが苦手な人のためにポイントをもとにした解きかたを説明します。
ポイント④:立方体で頂点Aからもっとも遠い頂点Gは、展開図では、正方形を2つ並べて長方形を作って頂点Aから対角線を引いた先の頂点Gとなる。
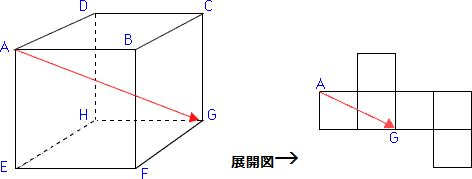
もちろん、このきまりは、立方体のどんな展開図についてもあてはまります。
このきまりを発展させて、対角線(ここでは→)をさらに引くと、次のこともわかります。
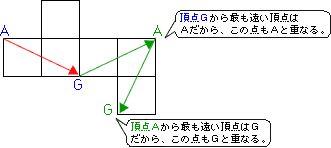
(1)
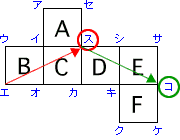
エから最も遠い頂点はポイントよりBとCを並べた長方形に対角線を引いてみるとスであることがわかります。
答え ス
(2)
スから最も遠い頂点がエになるので、さらに対角線を引いてみると、コであることがわかります。
答え コ
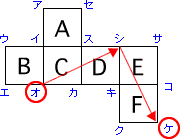
(3)
オと重なる点も同様に考えると、ケであることがわかります。
答え ケ
(4)
ポイント①、②よりAを上面とすると、Fが下面になるので向かい合う。(平行になる)
答え F
(5)
これまで同様にケとコが重なる点を考えて重なる辺をみつけだすこともできますが(別解図参照)、次のようにしてポイント③を活用して、Fの90°回転を繰り返すことによりケコと重なる辺を見つけだすことができます。
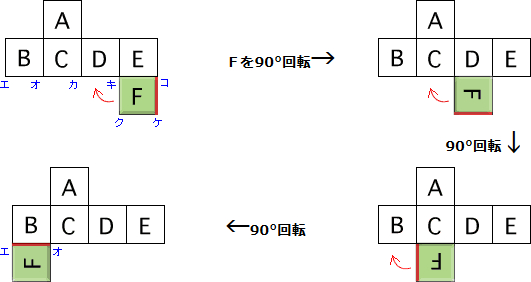
辺エオと重なる
答え エオ
(別解図)
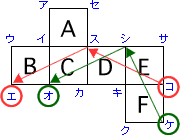
今回4つのポイント(②と③が同じなので実質的には3つ)で説明しましたが、頭の中のイメージで解ける問題も含まれていると思います。
これらのポイントは、イメージが苦手な人や得意な人でもイメージが難しい複雑な問題に出くわした時に、特に有効になります。

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事