例えば、10mの道に沿って、2mおきに端から端まで木を植えると次のようになります。

この図を見るとわかると思いますが、「木の数」は6本、「木の間の数」(区画の数)は5つとなっています。
「木の数」の方が「木の間の数」(区画の数)よりも1本多くなっていることが植木算のポイントです。
それでは、植木算の代表的な問題を解いてみましょう。
解法を見る

1周300mの池の周りに6mおきに木を植えることにしました。木は何本必要でしょうか。
解法を見る

図のようなP字型の道に2mおきに木を植えるとすると、全部で何本の木が必要でしょうか。
解法を見る

■ 答え
21本
 を一つの組み合わせとして考えるとよいでしょう。
を一つの組み合わせとして考えるとよいでしょう。

■ 答え
13本
■ 答え
50本

下図のようなP字型の道に2mおきに木を植えるとすると、 全部で何本の木が必要でしょうか。
これまでと同様に区画の数を割り算で計算してみます。

■ 解法
問題2と同様に解いてみましょう。
全長は、6×5=30m になります。
区画の数は30÷2=15 区画 です。
 を木とし、
を木とし、 を区画として
を区画として を一つの組み合わせで考えてみると、下図のようになります。矢印で示した通りに進んでいくと、最後の区画の先には、すでに木が植えてあります。
を一つの組み合わせで考えてみると、下図のようになります。矢印で示した通りに進んでいくと、最後の区画の先には、すでに木が植えてあります。
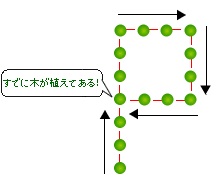
結局、問題3の池の周りに円形に木を植えた場合と同様に、区画の数と木の数が同じになります。
よって、必要な木の本数は15 本となります。
■ 答え
15本
※ 試してみるとわかりますが、問題2のT字型以外でも、H型やF型など円形を含まない道では
木の数=区画の数+1 となります。
また、問題4のP字型のように、円形を1つだけ含む場合は、
木の数=区画の数 となります。

この図を見るとわかると思いますが、「木の数」は6本、「木の間の数」(区画の数)は5つとなっています。
「木の数」の方が「木の間の数」(区画の数)よりも1本多くなっていることが植木算のポイントです。
それでは、植木算の代表的な問題を解いてみましょう。
![]()
100mの道に沿って、5mおきに木が植えてあります。何本の木が植えてあるでしょうか。
解法を見る ![]()
![]()
解法を見る

1周300mの池の周りに6mおきに木を植えることにしました。木は何本必要でしょうか。
解法を見る
図のようなP字型の道に2mおきに木を植えるとすると、全部で何本の木が必要でしょうか。
解法を見る

![]()
100mの道に沿って、5mおきに木が植えてあります。何本の木が植えてあるでしょうか。
■ 解法
まず、割り算で「木の間の数」(区画の数)を計算してみます。
100÷5=20
より、「木の間の数」(区画の数)は20あることがわかります。
木の数はこれより1本多いから21本です。

■ 答え
21本
![]()
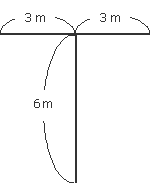
図のようなT字型の道に1mおきに木を植えると、 全部で何本の木が必要でしょうか。

■ 解法
全長は、3+3+6=12m になります。
区画の数は12÷1=12区画です。
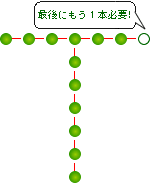
![]() を木とし、
を木とし、![]() を区画として
を区画として![]() を一つの組み合わせで考えてみると、下図のようになります。
を一つの組み合わせで考えてみると、下図のようになります。
結局、ここでも、区画の数よりも1本だけ多く木が必要になります。
よって、必要な木の数は12+1=13(本)

■ 答え
13本
![]()
1周300mの池の周りに6mおきに木を植えることにしました。木は何本必要でしょうか。
■ 解法
これまでと同様に区画の数を割り算で計算してみます。
300÷6=50
より、区画の数は50あることがわかります。
木の数はこれより1本多いから51本としてしまうのは間違いです。
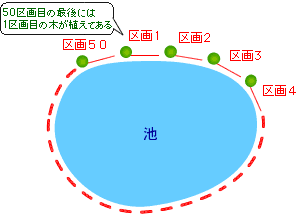
下の図のように、円形に木と区画の組み合わせ![]() を考えていくと50区画目の最後には、1区画目の木が植えてあることがわかります。つまり、円形に木を植えていくときは、植える木の数と区画の数が同じになるのです。
を考えていくと50区画目の最後には、1区画目の木が植えてあることがわかります。つまり、円形に木を植えていくときは、植える木の数と区画の数が同じになるのです。
よって、必要な木の本数は50本です。
木を 、区画を
、区画を であらわします。
であらわします。

■ 答え
50本
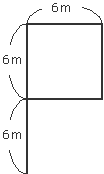
下図のようなP字型の道に2mおきに木を植えるとすると、 全部で何本の木が必要でしょうか。
これまでと同様に区画の数を割り算で計算してみます。

■ 解法
問題2と同様に解いてみましょう。
全長は、6×5=30m になります。
区画の数は30÷2=15 区画 です。

結局、問題3の池の周りに円形に木を植えた場合と同様に、区画の数と木の数が同じになります。
よって、必要な木の本数は15 本となります。
■ 答え
15本
※ 試してみるとわかりますが、問題2のT字型以外でも、H型やF型など円形を含まない道では
木の数=区画の数+1 となります。
また、問題4のP字型のように、円形を1つだけ含む場合は、
木の数=区画の数 となります。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
