既習を生かして「なるほど!」を作り出す<3年:分数のひき算> 「はてな?」「なるほど!」「だったら…」で作る算数授業(第4回)
分数は子供たちにとって理解の難しい学習の一つです。第4回では、3年「分数のひき算」の授業実践を紹介します。
小数と分数を関連させて「なるほど!」を引き出す
分数には次の5つの意味があると現行の学習指導要領解説に明記されています。
- 分割分数(2年生で学習)
- 量分数(3年生で学習)
- 単位分数(3年生で学習)
- 割合分数(5年生で学習)
- 商分数(5年生で学習)
しかし、日常生活では、習う学年など関係なく使われ、会話で単位を省略することも多いため、子供たちの理解を難しくしているようです。
また、分数を1つの数と見なすことが難しいことも挙げられます。例えば、「 1 4 + 2 4 = 3 8 」と考える誤答は、分母と分子の数字をばらばらに見ていると考えられます。また、同値分数である 1 3 と 2 6 を等号で結べないケースは、表記が違うことで違う数の大きさとして捉えてしまうと考えられます。
ドリルなどの反復練習を多めに取り入れても、その直後は修正されますが、実感を伴った理解には結びつかないせいか、時が経てばまた元に戻ってしまう子を多く見かけました。
このように、長い間私も分数指導で悩んでいました。そんな中、『だから「小数と分数」は一緒に教える』(2008年発行・東洋館出版社・現在は入手困難)という本に出合いました。
この本は成城学園初等学校で行われていた「小数と分数を関連させた学習指導を考える」というテーマに基づいた研究実践をまとめた本です。特に参考になった内容を下記にいくつか挙げます。
- 今まで別々の単元で教えていた小数と分数を同じ単元内で扱うことによって、同じ数と理解したり必要に応じて分数を小数に変換したりして、問題解決に生かすことができる。
- 分数で難しかった計算のきまりの活用が、小数と分数を関連させて学習することにより小数でできたことは分数でもできると考え、「分数のわり算」で自ら活用する子が増える。
- 小数で理解しやすかった「単位の考え」が、分数でも同じように考えるようになる。
この本があまりにも面白かったので、成城学園初等部の授業研究会に参加しました。
その中で、『生かす算数・生かす数学シリーズ』のテキストがこの本の作成に大きく関係していることを知り、手に入れました。
これは、杉山吉茂先生(東京学芸大学名誉教授)を中心に研究開発を進めてきた「わが国の算数・数学の望ましいカリキュラム構想(日本教材文化研究財団、2003年)」を具体化し、小学校4年生から高校までのテキストにしたものです。
中を見ると、小数と分数を関連させた内容だけでなく、約20年前にもかかわらず表計算ソフトを使った内容が扱われていました。また、小数や分数をかけるかけ算では、比例数直線を用いての「倍比例」「帰一法」の考え方や、「計算のきまり」を活用した解決も丁寧に扱われていました。
次の学習指導要領では、「中核的概念」がテーマになったり、40分授業が実施できたりするようです。少なく教えて多くを学ばせたい算数授業を目指している方は、ここで紹介した本はとても参考になることでしょう。
※日本教材文化研究財団『生かす算数・生かす数学シリーズ』
現物は入手困難とのことですが、日本教材文化研究財団より閲覧用のPDFを提供いただきました。こちらからダウンロードして、閲覧できます。私的な範囲に限ってご利用ください。
3年「分数のひき算」
今回紹介する「分数のひき算」は、小数と分数を関連させた実践のひとつです。
同分母同士のたし算とひき算なので、わざわざ小数に置きかえる必要がないと考えるかもしれません。
しかし、分数をまだ数として見なしていない子がいることを踏まえると、なじみのある小数で計算を確かめることによって、実感を伴った理解につなげることができます。また、子供たち自身で「分母はそのままで分子だけ計算する」と気付き、計算方法をまとめることができることができます。
さらに、たし算・ひき算で小数と分数を関連させることで、今後のかけ算やわり算でも同様に考える態度を育てることにもつながります。
授業の様子
はてな?
前々時で「分数のたし算」を、小数と分数を関連させて学習しました。(前時は分数のたし算の計算練習)
その振り返りに、「分数のひき算もできそう」と書いたAさんのノートを紹介し、黒板に下記の3つの問題を書きました。
3
5
-
1
5
7
10
-
4
10
1 -
1
2
そして、みんなに挑戦するかどうかと問いかけると、
「できそうな気がする!」
「やってみたい!」
と声が上がりました。
このように、前に書いた振り返りを導入で使う方法は、短い時間で本時の学習に対して関心・意欲が高めることができるため、とてもお薦めです。また、第20回 で取り上げた「算数・数学の学習過程のイメージ」のD2(「結果」から「数学の事象」へ)となり、問いが連続する授業となります。
なるほど!
まず「
3
5
-
1
5
」の問題に取り組みました。
この問題を設定したのは、前の学習の問題「
1
5
+
2
5
=
3
5
」を「0.2+0.4=0.6」と見たことを生かすことができると考えたからです。机間巡視すると、予想通り子供たちのノートには、「0.6-0.2=0.4」の記述がほぼ全員にありました。
どうやって計算したか、Bさんに発表させました。
Bさんは黒板に「0.6-0.2=0.4」の式を書き、次のように説明しました。
「小数に直したら答えが分かるから、分数を小数に直しました。0.4は
2
5
なので、答えは
2
5
です。」
その説明を聞いてみんなが頷いています。そんな中、Cさんが「付け足しがあります!」と手を挙げたので、発表させました。
「56番の図を使って、分数を小数に直しています。」
この「56番」というのは、毎回の授業でノートに書いている通し番号のことです。今回の授業の板書の写真では、日付の右に丸で囲んである「62」がそれにあたります。
以前は、既習内容を確認するとき、教科書のページを発表させていました。しかし、教科書には知識のみ表記されているため、見てもなかなか思い出すことが難しい子が多かったです。そこで、はじめたのがノートを使って既習内容を確認する方法です。ノートを使うため、その時の学びのエピソードが蘇るようで、既習内容を思い出す子が増えました。
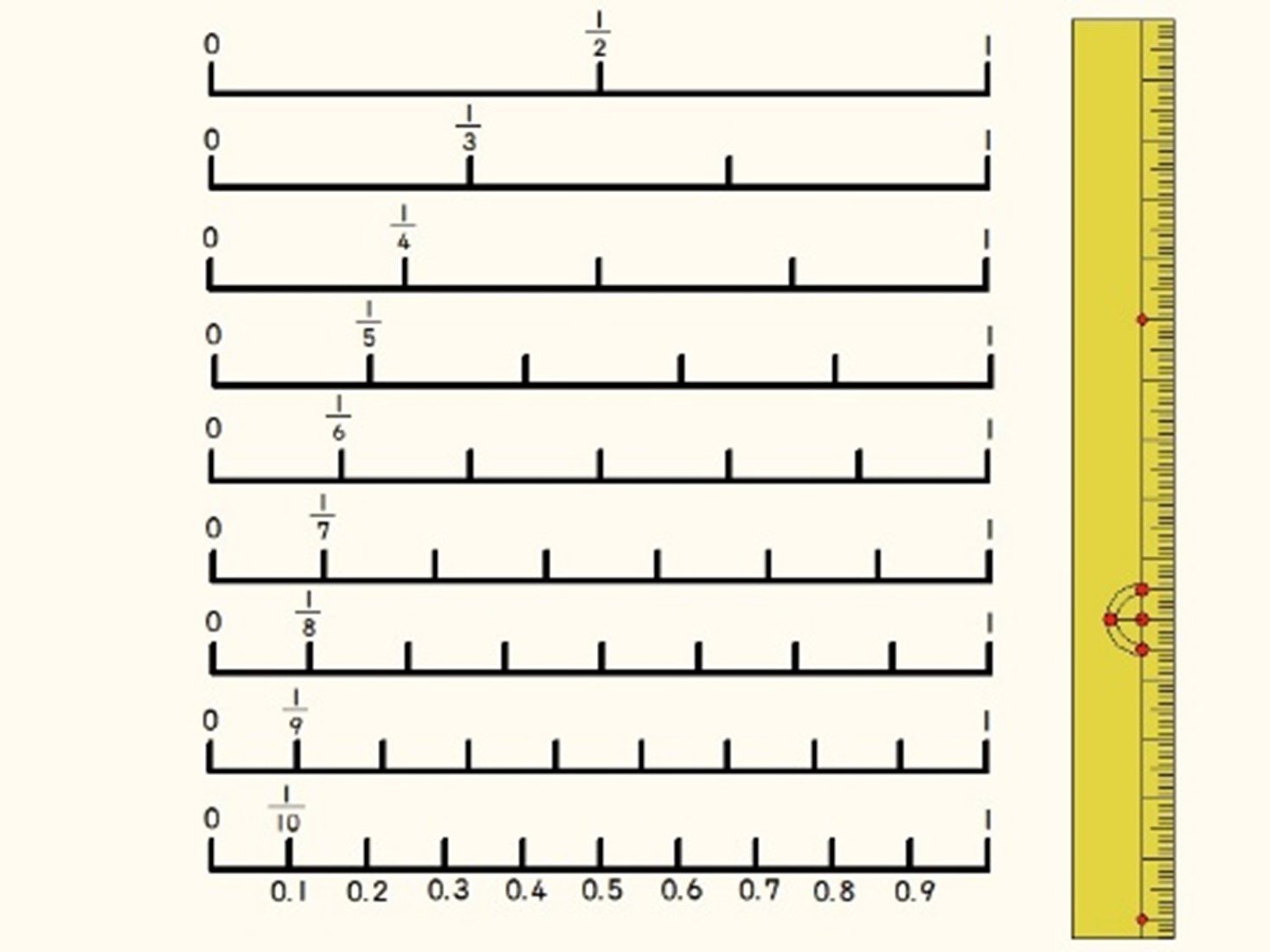
なお、「56番の図」というのは、 1 2 から 1 10 の分数の線分図を並べた図を指しています。 1 10 の線分図には、下の方に対応する小数も表記しています。 この線分に定規をあてることで、分母が違う分数の大きさを比べたり、同値分数や小数を探したりすることができます。
次の問題「 7 10 - 4 10 」も、その次の問題「1 - 1 2 」も、分数を小数に直して答えを求めることができました。
だったら…
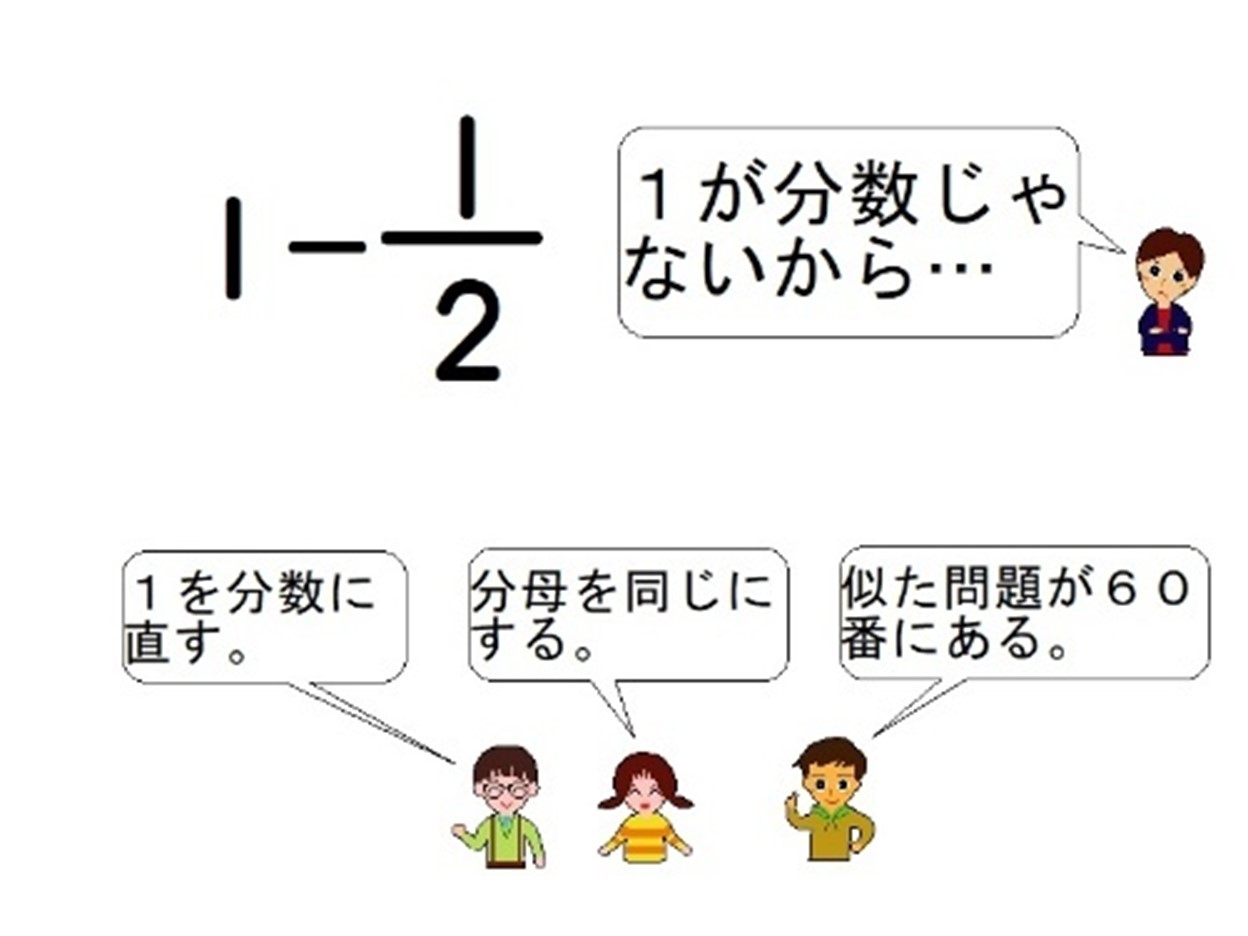
Dさんが隣の子に
「分数だけでも計算できるよ!」
とつぶやいている声が聞こえました。
Dさんに、どうしてそう考えたか聞いてみました。
「分数のたし算の時はできたから、ひき算でもできるかどうか考えたら、同じやり方でできた。」
Dさんの話が分かった人を確認すると、ほとんどの人が手を挙げましたが、数人は首を傾げています。
その中の一人、Eさんに分からない部分を言ってもらいました。
「『1』は、分数じゃないから…。」
算数授業では、分からない人の言葉に耳を傾けることが大事です。その言葉に寄り添い、その子が分かるように説明できる子を育てることが、楽しい算数授業の基盤になります。
「Eさんのために、いいヒントが出せないかな?」
と問いかけました。3人が発表してくれました。
「『1』を分数に直す。」
「分母を同じにする。」
「似た問題が60番にある。」
これらを聞いてEさんの表情が明るくなったので、分数のひき算のやり方を発表させました。
「1は
2
2
にします。そして、分母はそのまま、分子を引きます。」
自然に拍手が起きました。
残り5分になったので、振り返りの時間を取りました。机間巡視でノートを見ると、下記のような単位分数で考えている記述があったので紹介して終わりました。
「
3
5
-
1
5
」は
1
5
で考えると3―1=2、だから
2
5
」
次回は、6年「分数のわり算」を取り上げます。お楽しみに!

種市 芳丈(たねいち よしたけ)
小中一貫三戸学園 三戸町⽴三戸⼩学校・三戸中学校 教頭
子供たちが夢中になる算数授業づくりに取り組んでいます。算数専科や複式学級の指導の経験あります。今、チャレンジしているのは、ロイロノートを活用した算数授業です。算数の教材づくりの会「ガウスの会(代表:細水保宏)」の会員。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生





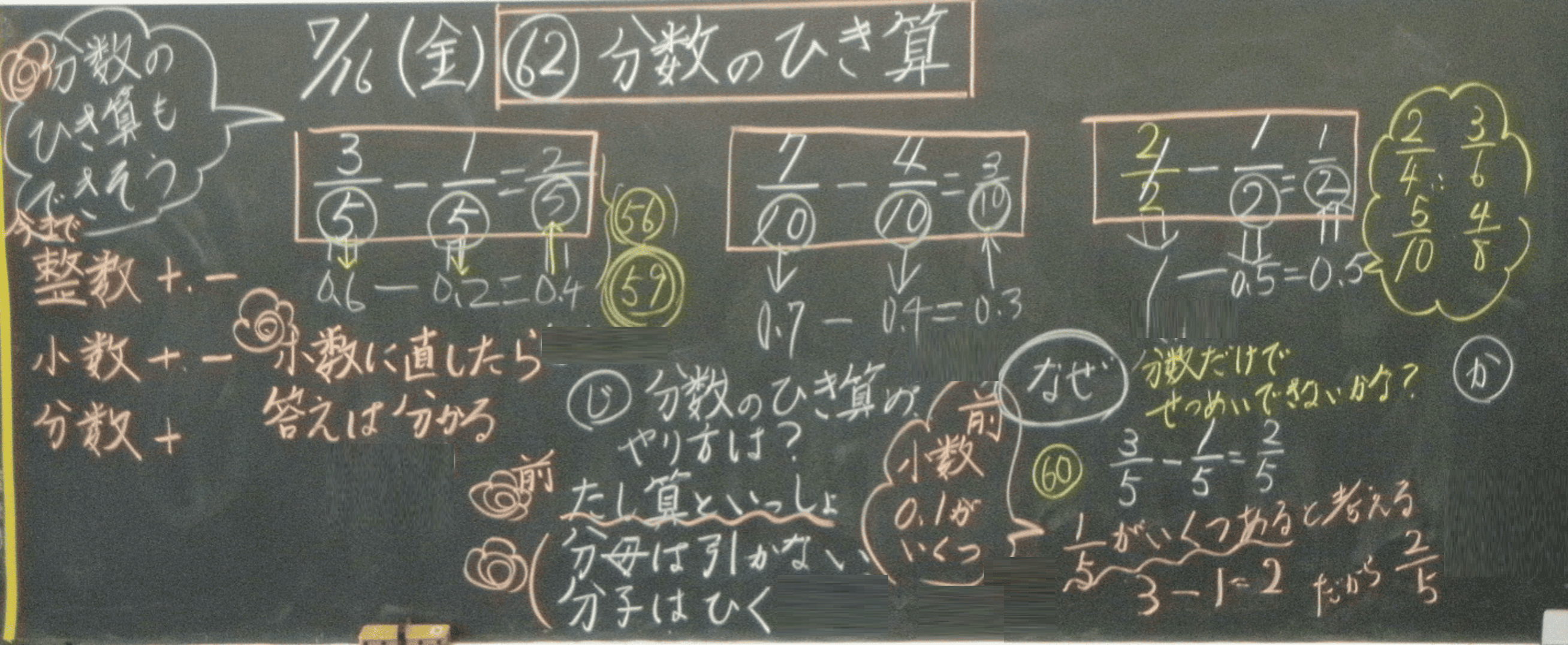
 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
