算数手品で「はてな?」を引き出す2<3年:かけ算の筆算> 「はてな?」「なるほど!」「だったら…」で作る算数授業(第3回)
第3回では、3年「かけ算の筆算」をしたくなる教材と、その授業実践を紹介します。
かけ算の筆算をしたくなる教材
かけ算の筆算には、「かけ算」「(繰り上がりのある)たし算の筆算」の2つの計算技能の定着が不可欠です。どちらか一方にでも苦手があると、計算に時間がかかったり、練習になかなか取り組まなかったりします。だからといって、苦手克服のためのかけ算九九やたし算のプリントばかりでは、かえって意欲も落ちがちです。
そこで、私は単元の途中や終わりに、かけ算の筆算をしたくなるような教材に取り組ませてきました。不思議なもので、かけ算の筆算自体に面白さを感じると、進んで計算練習する子が増えるからです。
第27回で、下記のようなかけ算の筆算をしたくなるような教材を紹介しました。
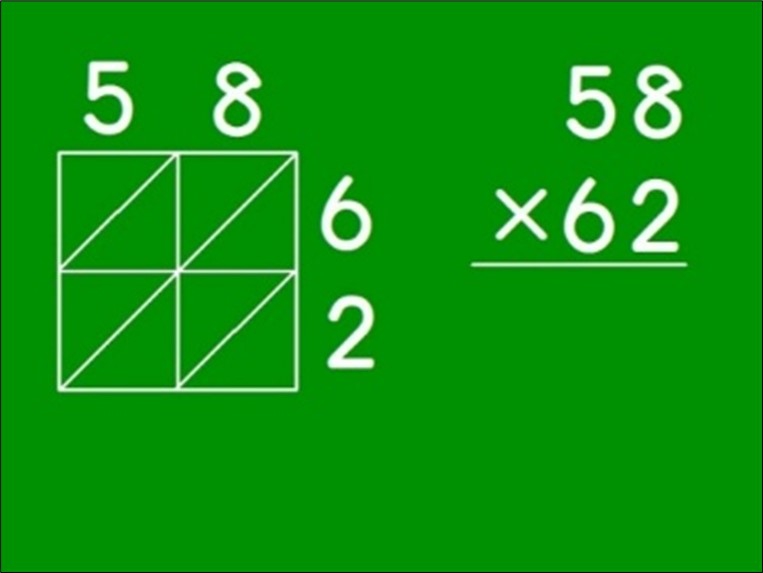
- 格子かけ算(スクプレ教材)
2桁同士をかける「格子かけ算」を知り、かけ算の筆算と比べさせることで、計算の仕組み考えたり、3桁×2桁など適用範囲を広げたりする教材。 - 線を引くだけの筆算(スクプレ教材)
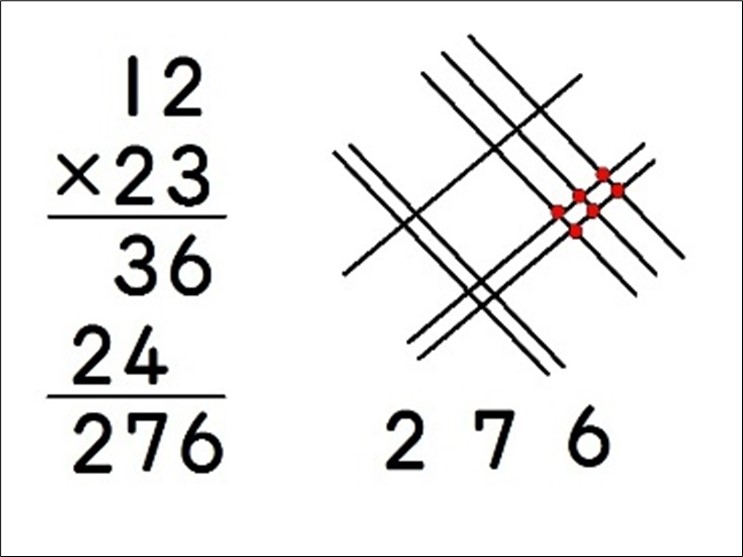
インドなどで行われている線を引くだけでできるかけ算の筆算を、自分たちが学習したかけ算の筆算と比べさせ、共通部分があることに気付かせる教材。 - 速算のカード(スクプレ教材)
先生と子供たちで計算競争すると、先生がいつも勝つことから、「何かひみつであるかも…」という気持ちを 引き出すことかできます。ひみつを見つけたら、自分で式を作る活動に発展させることのできる教材。
動画「ちがいがすぐ分かる」
今回紹介する「ちがいがすぐ分かる」も、そのような教材の一つです。連続する2つ数にそれぞれの数をかけて差を出す計算競争を先生と子供たちで行うと、必ず先生が勝つという教材です。
例えば、「98」と「99」だと下記のような計算になります。
99×99-98×98=9801-9604=197
かけ算の筆算を2回、その後、繰り下がりのあるひき算の筆算をするので、かなりの計算量になりますが、先生はある秘密さえ知っていれば、簡単な暗算ですぐ答えが出せます。
その秘密は、「連続する2つ数の和」です。上の例だと、「99+98=197」です。
これは文字式で証明できます。
aとbは連続する数なので、a=(b+1)で表せる。
a²-b²=(b+1)²-b²
=2b+1
=(b+1)+b
=a+b
つまり、連続する数の和と等しい。
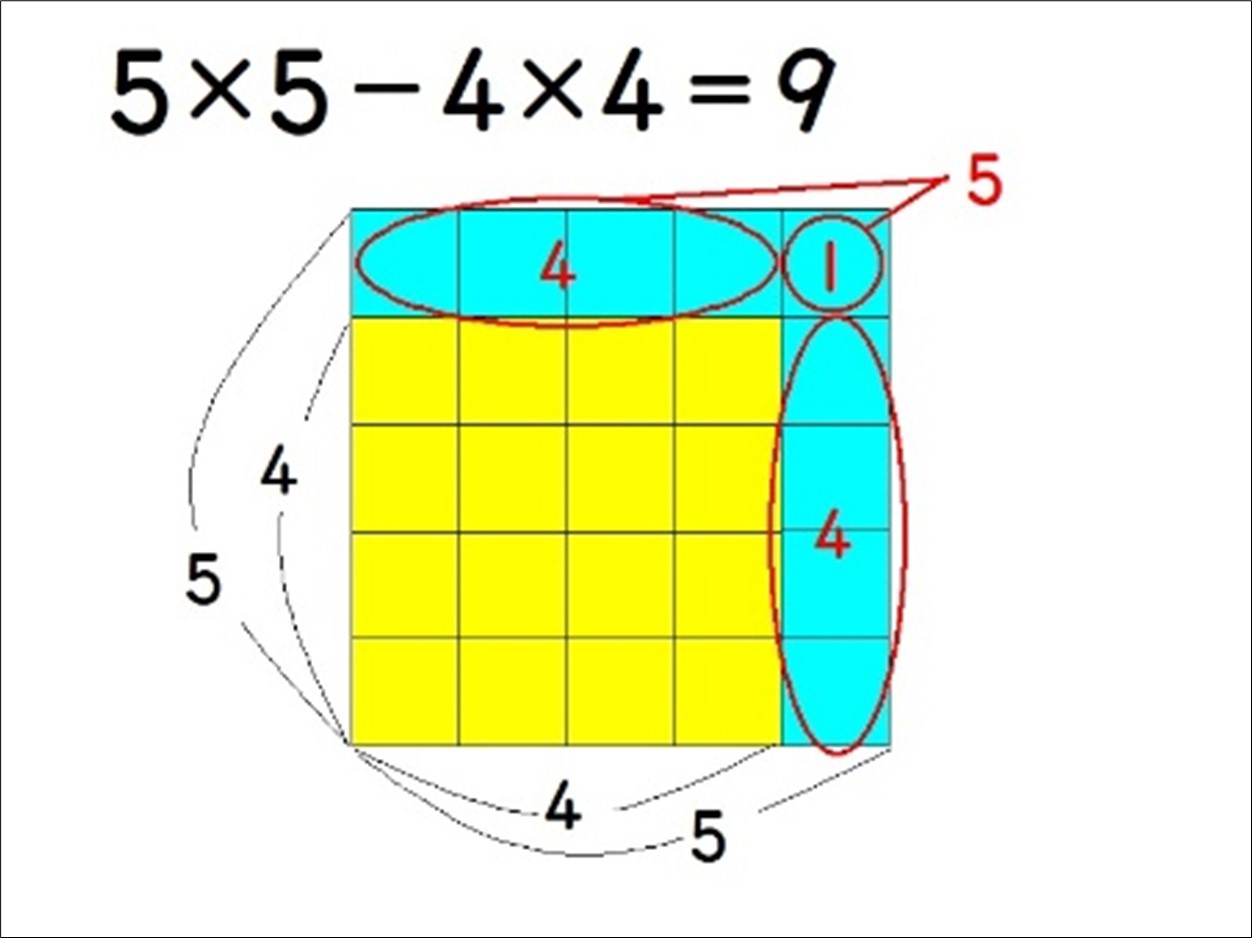
図1
これは小学生には難しいですが、図1のような面積図であれば、理解できる子がいるでしょう。
5×5-4×4=25-16
=9
=(4+1)+4
=5+4
補足になりますが、きまりのある教材を授業で扱うときは、「なるほど!」で小学生でも理解できるものを準備しておくことが大切です。小学生が理解できる説明が準備できない教材は、「なるほど!」が生まれないため、算数の教材としては相応しくないと考えています。
下記の「授業の様子」で紹介する実践は、算数手品として授業で扱ったため、子供に決めさせた数値「98と99」や「22と23」で授業を展開しました。算数手品なので子供が意欲的に取り組みましたが、子供が考えた数値のため面積図にするには難しくなってしまいました。
そこで、「2と3」や「4と5」などの簡単な数値にして面積図で説明しました。そのため「簡単な場合で考える」という数学的な見方・考え方が一つ加わった授業となり、理解が難しくなった子がいたことは事実です。
その反省を踏まえ、『授業で使える! 算数おもしろ問題60』(東洋館出版)で、同じ教材を取り上げた際は、「14と15」など連続する数の和が見えやすく、かつ、そのままの数値でも面積図で表現できる数値にして問題を掲載しました。
なお、この本では、かけ算の筆算をしたくなる教材として、下記の問題も掲載されています。さらに教材研究をしたい方は、御一読ください。
- 12 一番大きくなる式は?
連続する3つの数字で2桁×1桁を考えたとき、答えが一番大きくなる式を考える。 - 16 同じ数字が並ぶには?
37×□の答えを考えたとき、同じ数字が並ぶきまりを考える。 - 19 入れ替えても答えは同じ?
2桁×2桁の計算をしたとき、十の位と一の位を入れ替えても同じ答えになる式を考える。
授業の様子
はてな?
まず、黒板に「ちがいがわかる」と書いて、次のように言いました。
「『先生』対『みんな』で2桁のかけ算を使った計算競争をしようよ!」
このクラスで算数を教えてもう9か月経っているため、子供たちの最初の反応はこうでした。
「あやしい…。」
「何か新しい算数手品を思いついたんでしょ…。」
盛り上がるには少しかける雰囲気です。そんな時は、少し子供たちとやり取りをして気持ちをほぐしていきます。
「じゃあ、やめよう!えっと計算ドリルの…。」と計算ドリルを開こうとすると、
「待って、待って!」
「新しい算数手品が見たくなってきた!」
「計算ドリルよりこっちの方がワクワクするから好き。早く始めて!」
お互いに気持ちが整ったので、算数手品を始めました。
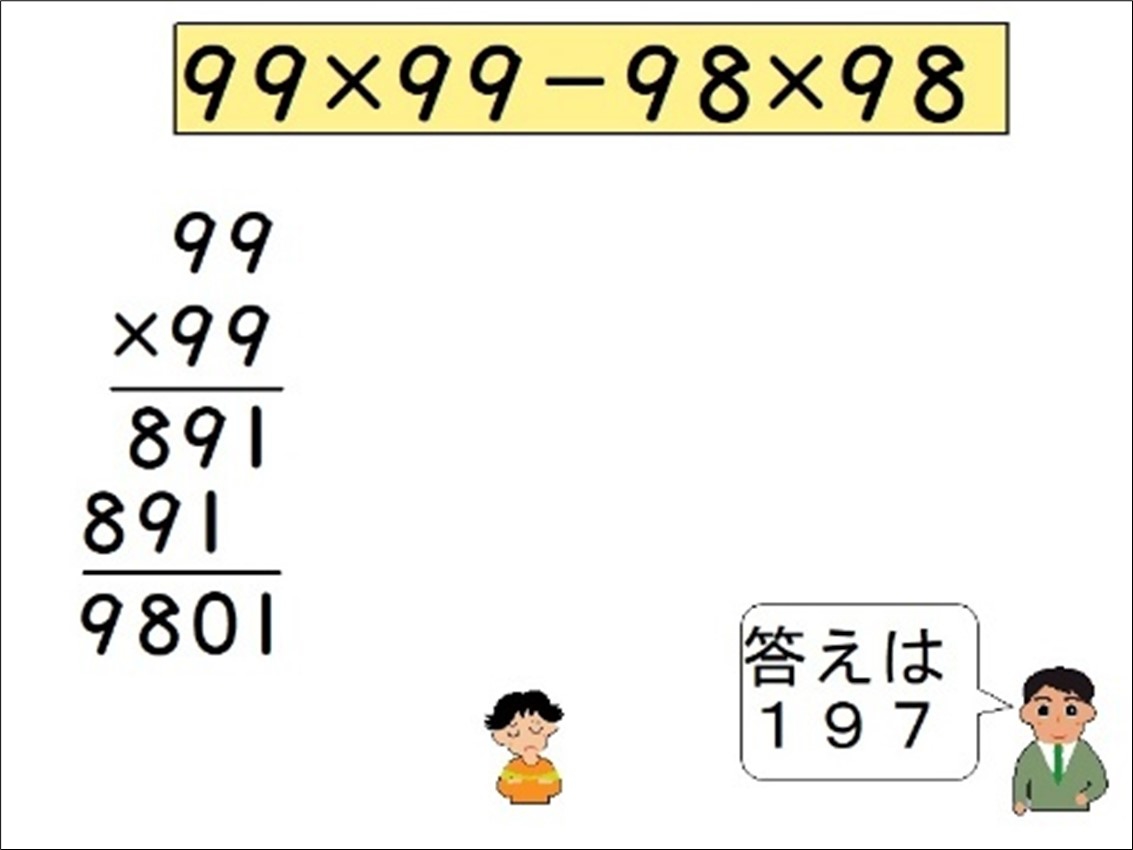
まずAさんに連続する2桁の数を選んでもらいました。
「99と98。」
「では、この数を使って、連続する2つ数にそれぞれの数をかけて差を出す計算をします。この場合たと、『99×99-98×98』ですね。」と説明し、計算競争をスタートさせました。
どの子も『99×99』の筆算の計算し始めた頃は見計らって、
「198かな?」と聞こえるようにつぶやきました。
しばらくすると、次々に驚きの声が上がりました。
「…合ってる!なんで?」
「先生、速すぎない?」
「もう一回、やろうよ!」
計算の速い子は意欲が高まってきましたが、まだ計算途中の子もいます。
ここでのポイントは、全員が自分で計算することです。計算して驚いた子と、ただ計算をしないで傍観していた子では、このあとの動きが全く違うからです。
一度机間巡視をしたところ、まだ10人は計算途中でした。もう少し時間が必要です。
早く確かめた子たちをじっと待たせるのではなく、知らないうちに待っていたことにするのは教師の腕の見せ所です。今回は、既に計算が終わった子たちと、黒板にこの計算を確認していきました。
そうしているうちに、次々に「本当だ!」と聞こえてきました。
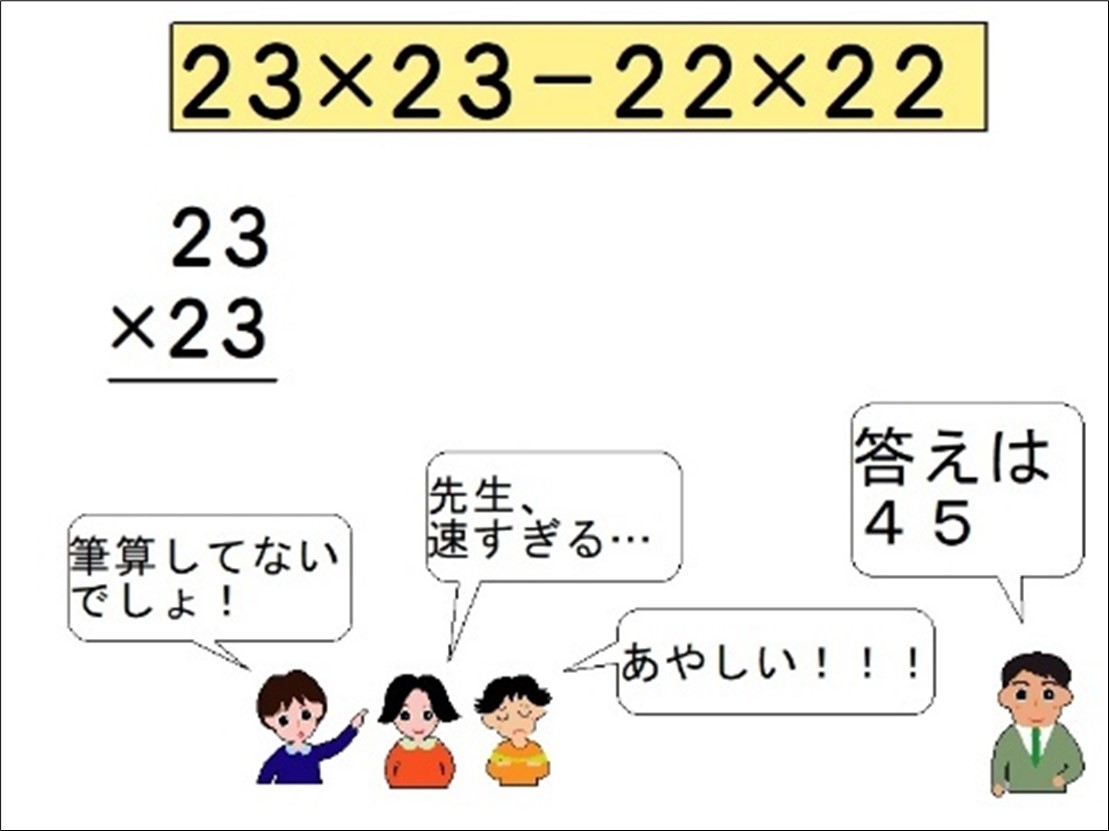
全員が自分で計算したことを確認してから、さっき「もう一回、やろうよ!」とつぶやいたBさんに連続する2桁の数を選んでもらいました。
「22と23。」
聞くや否や、既に計算を始めている子がいます。
ほかの子も計算をスタートさせた直後に、
「この答えは…45かな。」と言うと、
「先生、速すぎる…」
「筆算してないでしょ!」
「あやしい!!!」
筆算しながら、声が上がりました。
先ほどと同じように、早く終わった子たちと、黒板に計算の確かめ(23×23-22×22=45)をし、45になることを確認しました。
なるほど!
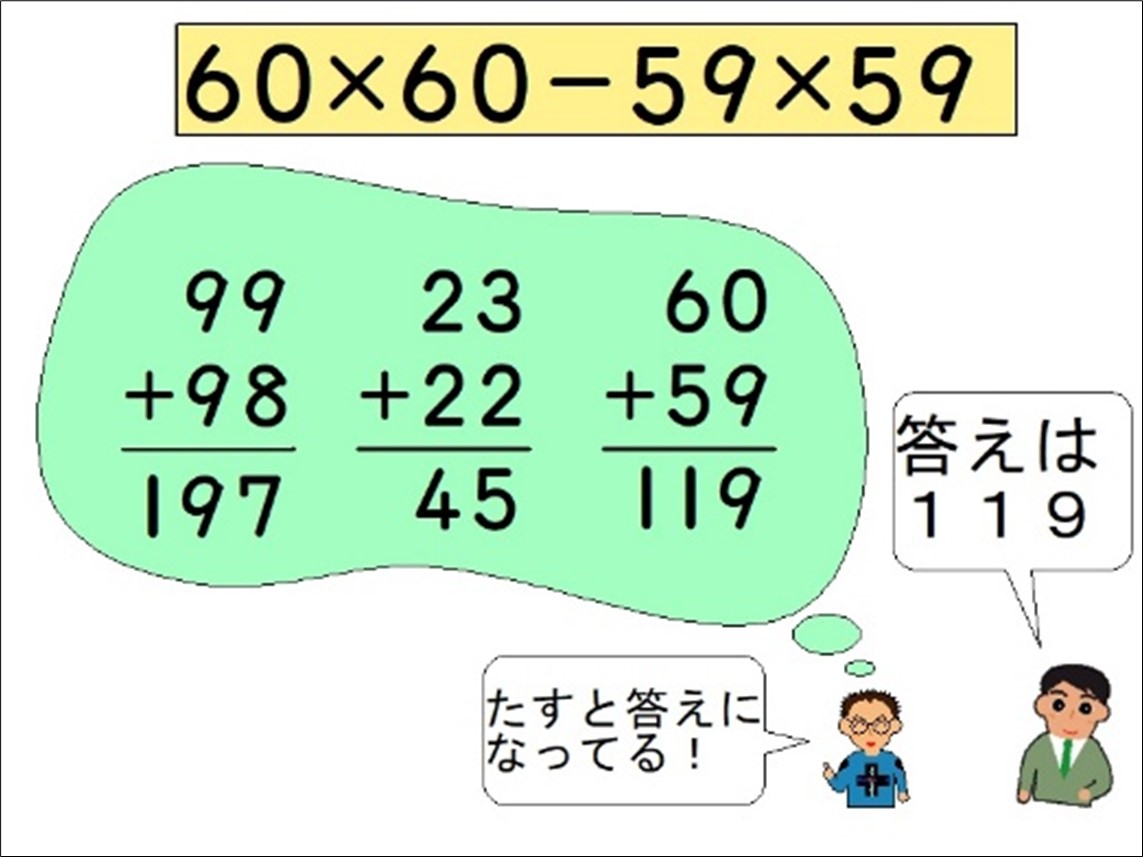
3問目に取りかかろうとした時です。
「先生、2人選んでください。」とCさんが言いました。理由を聞いてみます。
「一人は『数を決める人』、もう一人は『先生を観察する人』です。」
面白いことを考えると思いました。何より、自分たちで何とか「あやしい!!!」を解決するために動き出しているところがいいです。
Cさんを『先生を観察する人』、Dさんを『数を選ぶ人』にしました。
Dさんが「59と60」と言うのに合わせて、みんなは一斉にノートに計算を始めました。でも、Cさんだけはじっとこちらを見ています。
少しでもヒントになるよう、大袈裟に上の方を見上げながら小さな声で「59と60」とつぶやき、少し間をあけて「119かな。」と言ってみました。そして、Cさんの目をじっと見て、にっこり笑ってみせました。
Cさんは、黒板に書いてある「99×99-98×98」と「23×23-22×22」の計算をじっと見たかと思うと、
「たすと答えになってる!」と教室に響き渡る声で言いました。
しばらくして、「60×60-59×59」を終えた子たちから「119」になっていることに驚きの声が上がりました。
Cさんは計算を終えた子たちに向かって、説明を始めようとしました。
「時間よ、止まれ!」と静止しました。
第2回でも使った手法です。Cさんがすべてを話してしまい、各自で気付く喜びを奪ってしまうにではないかと考えました。
そこで、Cさんにはみんなも気付くようなヒントを一文で考えてもらい、その間に、終わった子たちと黒板に計算の確かめをしていきました。
さあ、Cさんからヒントの発表です。
「式のどこかをたすと答えになる。」
教室が静かになりました。
これは、みんなが真剣に考えはじめると起きる現象です。この沈黙に教師が耐えられず、先生からさらに追加のヒントを出してしまう授業を見かけますが、それは悪手です。せっかく真剣に考えているのに水を差すだけてなく、待てば先生が何とかしてくれるという受け身の子を育ててしまいます。考える楽しさを感じられる子供を育てる気持ちで、教師はあえて「待ちの姿勢」を取るのが好手です。
「…そうか!」
「…本当だ!」
次々に声が上がりました。自分で気付いた子は笑顔になります。でも、そんな声にも、必ず困った顔をしている子が数人いるものです。教師はそのような顔をした子がいないか、子供たちの表情をじっと観察します。
やはり、3名ほどいました。
その子たちのために、Fさんには、Cさんのヒントは板書のどの部分を見ればいいのか黒板に書き込んでもらいました。
「99」「98」「197」を丸で囲み、次に、「23」「22」「45」も丸で囲んだ時です。先ほどの3名の一人、Gさんが、
「先生、続きをやりたい!!!」と挙手しました。
啐啄同時*のチャンスです。Gさんに続きをやってもらいました。
「60」「59」「119」を丸で囲んだ後、うれしそうに席に戻っていきました。
だったら…

時計を見ると、あと7分でチャイムが鳴ります。面積図の説明の時間を取りたいので、少し早めに振り返りの時間にしました。
「みんな、すごいなあ!新しく考えた算数手品のタネがあっという間にばれてしまいました…。でも、なぜ、連続する数をたすと、答えになるのかな?もし、分かった人がいたら、振り返りに書いてください。もちろん、いつものように、今日の勉強を使ってやってみたいことや似ていると感じたことを、『だったら…』の書き出しで書きましょう。」
子供たちに「なぜ」の説明は難しいと思いましたが、もしかしていいアプローチをする子がいるかもしれない…と思い、考える場を取りました。
机間巡視をしましたが、「なぜ」について書いた記述は見つけられませんでした。
「だっだら」については、「3ケタや4ケタの計算でもできそう」や「電卓と競争してみたい」などが書かれていました。
最後に、子供たちの手を止めさせ、面積図を使って「3×3-2×2=5」と「5×5-4×4=9」を説明し、授業を終えました。
次回は、3年「分数のひき算」を取り上げます。お楽しみに!

種市 芳丈(たねいち よしたけ)
小中一貫三戸学園 三戸町⽴三戸⼩学校・三戸中学校 教頭
子供たちが夢中になる算数授業づくりに取り組んでいます。算数専科や複式学級の指導の経験あります。今、チャレンジしているのは、ロイロノートを活用した算数授業です。算数の教材づくりの会「ガウスの会(代表:細水保宏)」の会員。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生




 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
