既習を生かして「なるほど!」を作り出す2<6年:分数のわり算> 「はてな?」「なるほど!」「だったら…」で作る算数授業(第5回)
分数の学習の中でも、最も指導が難しいのが「分数のわり算」です。第5回では、6年「分数のわり算」の授業実践を紹介します。
わり算や分数の性質を生かして、子供自ら計算の仕方を作り出す
難しさの要因として下記が挙げられます。
ア 日常生活に分数のわり算が必要になる場面が少ない。
イ 説明に使われる面積図が分かりにくい。
ウ 既に「逆数をかける」ことを知っているため、計算の仕方を考えようとしない。
エ 考えのもとになる「わり算や分数の性質」が身に付いていない。
上記のアとイについては、ほとんどの教科書では塀のペンキ塗りの場面で単位量当たりの量を求める問題として扱い、面積図との接続をスムーズにできるようにしています。しかし、ここで扱われる面積図が、塀の面積とペンキの量を同時に扱うため、一見すると子供にとっても大人にとっても大変分かりにくい図となっています。
また、ウについては、一度忘れてしまうと思い出すのが難しいため、計算ができなくなったり、しばらく経つと混乱して分数のかけ算まで逆数で計算したりという子をよく見かけます。自分で計算の仕方を考えた経験があれば、忘れても関連した知識から導くことが可能ですが…。
エは、この単元の前までに培う力です。「わり算のきまり」とは、わり算ではわられる数とわる数に同じ数をかけてもわっても商は変わらないきまりのことです。4年生の「2けたのわり算」や5年生「小数のわり算」などで活用されていますが、教師が顕在化させないと筆算の手順の中に埋もれがちです。「分数の性質」とは、同値分数や商分数、単位分数、逆数などがこれにあたります。これらは計算練習だけで身に付けることは難しいです。
このようなことから、私も「分数のわり算」の指導で悩んでいました。そんな中、『力がつく算数科教材研究法』(1990年発行・明治図書出版・絶版)を紹介していただきました。
この本は、前回も紹介させていただいた杉山吉茂先生(東京学芸大学名誉教授)が、「算数教育」に連載していた内容をまとめたものです。特に参考になった内容をいくつか下記に挙げます。
- 35年前の本であるにもかかわらず、「新しい問題に直面した時、これに意欲的に取り組み、ねばり強く考え、これを解決し、これをもとに新たな課題を設定し、自ら創造的に学習する子」という現在の学習指導要領に通じる子供像を念頭に置いて書かれている。
- 「分数のわり算」の計算の仕方には、①「分母÷分母」「分子÷分子」で計算する、 ②通分して整数のわり算にする、 ③除数と被除数に除数の分母をかけて、÷整数にする…など、5つほど挙げられ、子供が自ら考えるのにどんな知識が必要か整理されている。
- 「かけ算の意味の拡張」をついて、具体的な事例が載っている。
このような名著ですが、私が知ったときには既に絶版で入手困難でした。そのため、本をもっている知人から借りて、全ページをコピーして使っています。
ところが最近、「復刊投票」があることを知りました。これは、明治図書出版で絶版になった書籍のうち「復刊投票する」というボタンがある本は、30人投票すると復刊する仕組みです。投票した人は復刊したら購入することが条件となっています。早速、『力がつく算数科教材研究法』に投票しました。現在、あと14票で復刊となっています。
最近、教育図書コーナーに行くと、「ICT」「働き方改革」「特別支援教育」などが目立ち、教科研究に関する書籍が少なくなったと感じます。算数授業をよくするには、素晴らしい算数教育の本に出合うことが重要です。よろしければ復刊投票していただき、この本に書かれている算数の授業観に触れてほしいと願います。
今回紹介する「分数のわり算」の実践は、下記の工夫をしています。
①図は比例数直線のみ
上記のアとイに対して、前単元の「分数のかけ算」から日常場面である塀を扱いませんでした。面積図は理解する以上に使いこなすのに慣れが必要だからです。そこで、日常場面を「小数のかけ算」や「小数のわり算」で親しんでいる鉄の棒にし、「
2
5
mで 3
4kgの鉄の棒があります。1mでは何kgですか。」という問題にしました。比例数直線との接続をスムーズにして図の活用を促しました。
上記のウに対してです。本時だけでなく、毎回に授業で培う態度になります。学級で理解したことを使って説明することを繰り返し指導していきます。前回紹介した既習の内容のノートの番号を書く取組は有効だと思います。もちろん、習ったことを使って説明できれば、逆数を使って構いません。 ③わり算や分数の性質の定着
上記のエに対してです。系統性の強い6年「分数÷整数」が、わり算や分数の性質が身に付いているか実態を把握するいい機会です。今回紹介する事例の子供たちは、「 4 5 = 12 15」という同値分数を活用するアイディアを持てた児童が少数だったので丁寧に指導しました。
授業の様子

はてな?
本時は、その意欲を生かして「『 3 4 ÷ 2 5』の計算の仕方を考えよう」と設定し、それぞれの考えを交流する場としました。
なるほど!
前時と本時まで時間があったので、子供たちのノートをじっくり見ることができました。
普段の授業であれば、自力解決の場面で机間巡視中にノートを見て指名計画を立てます。しかし、書き途中だったり、見た後に記述を修正したりしていて、時々ずれが生じてしまうことがありました。
例えば、写真のノートでは、机間巡視で見た時点では赤で囲んだ部分だけでしたが、ノートを回収して点検したときには、青い部分と黄色の部分が書き足されていました。
このような試行錯誤の様子を、交流場面の前に教師が把握して指名する授業と、授業が終わってからノートを集めて知ることでは、児童理解や教材解釈に大きな違いが出ます。自力解決段階でノートを回収し、書かれた内容をしっかり見取って次の授業に臨むのは大変勉強になるので、時々取り組むことをお薦めします。
子供たちのノートから、大きく3つの考え方があることが分かりました(複数回答あり)。みなさんなら、どれから取り上げますか?
①比例関係を使った逆数 (25/34人)
②比例関係を使って
1
5に戻して5倍(2/34人)
③最小公倍数20をかけて整数のわり算にする(11/34人)
考え方①
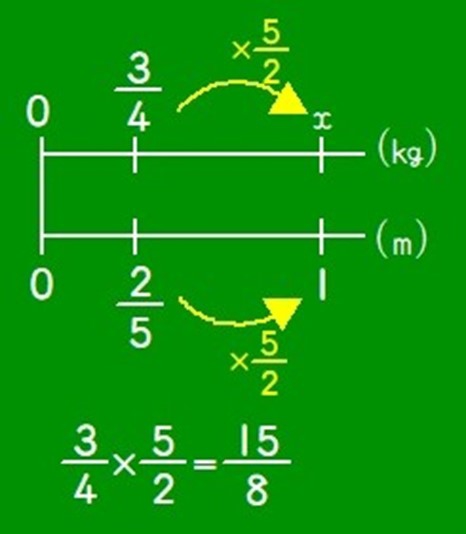
授業では、まず、①から取り上げました。理由は人数が多いこともありますが、先行知識で知っている「分数のわり算は、わる数の逆数をかける」が比例数直線を使うと説明がつき、残りの9人にも「なるほど!」という場面が生まれると考えました。
「発表してくれる人はいますか?」と問いかけ、まず①の考えを書いていたAさんを指名しました。
Aさんは、比例数直線を描きながら、説明を始めました。
「
2
5を1にするために×
5
2をします。それに伴って、
3
4
も×
5
2します。」
と言いながら、「
3
4
×
5
2 =
15
8」の式を書きました。
そこで、「もう一度、同じ内容を言える人はいますか?」と発問しました。
Bさんが続けて発表します。
「
2
5を1にするために逆数を使って×
2
5をします。それに伴って、
34
も×
5
2 します。」
「BさんはAさんの説明の言葉を付け足したね。何という言葉かな?」と発問しました。
一言一句、同じように説明する人はほぼいません。ほとんどの場合、どこかで内容の置き換えが起こり、大切な概念であることが多いです。これを利用し、今回は「逆数」という言葉を引き出すことができました。
Cさんが気付きました。
「『逆数』という言葉です。」
Dさんが続けます。
「44番や45番でも出てきました。」
この番号は、前回紹介した習った日のノートの通し番号です。そのページをめくって見直した子たちから、「そう、そう…」とつぶやきが上がり、既習内容とつながる様子が見られました。
考え方②
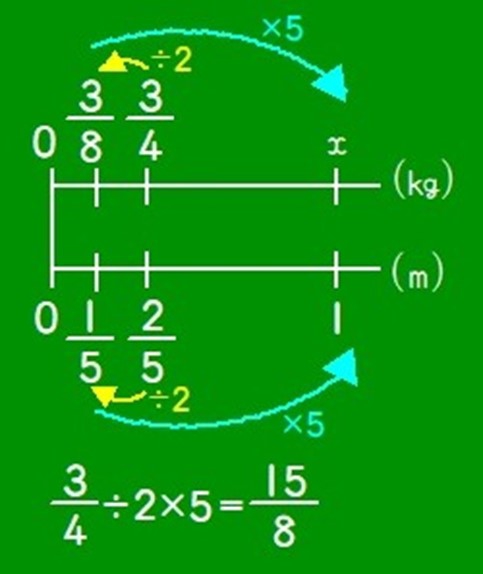
次に、人数は最も少ない②を取り上げました。このアイディアは「帰一法*」と呼ばれ、これまでの学習で何度も使われてきたアイディアです。前単元の分数のかけ算の計算の仕方を考えるときにも活用したことから、そのことを想起させれば、全員が理解できると考えました。
帰一法*…比例することがわかっている2量の関係について,その一方を1にしたときに他方がその何倍になっているかを考える方法
まず、「実は、逆数を使わないで解いた子たちもいました。」と問いかけました。ほとんどの子が逆数を使っていたので、
「気になる…、知りたい!」
「思いつかなかったなあ…、どんなやり方?」
と興味津々になりました。
②の記述をしていたFさんを指名しました。Fさんは黒板前に出てきて、比例数直線を描きながら説明を始めました。
「まず、 2 5を÷2をして 1 5を出します。それに伴って 3 4 も÷2すると 3 8になります。ここまでいいですか?」
Fさんは、聞いている人の分かり具合を確かめながら説明できる発表名人です。思わず、私も子供たちと一緒に「はい。」と返事をしてしまいました。
「次に、 1 5を1にするために×5をします。それに伴って 38 も×5すると 158 になります。どうですか?」
Fさんの発表の途中からGさんがノートをめくっていて、今、手を挙げました。
「先生、このやり方は41番でも出てきました。」
アイディアの根源が分かると理解が進みます。周りの子たちもノートをめくって確認すると、「なるほど…。」とたくさん声が上がりました。
Fさんは式を「 34 ÷2 = 3 8 、 3 8 ×5= 15 8 」と分けて書いたため、この後、統合的に見たとき逆数が見えにくいです。そこで、教師側から「1つの式にできるよね。」と投げかけ、下記のような式に表しておきました。
3 4 ÷2×5= 3 4 × 5 2 = 15 8
考え方③
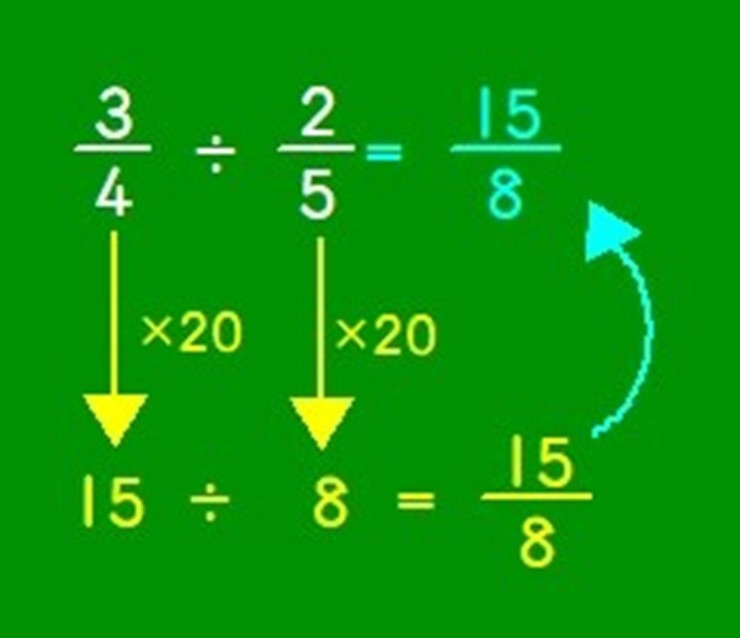
まず、「比例数直線を使わないで解いた子たちもいました。」と問いかけました。
「え?どういうこと?」
「見たい!聞きたい!」
と盛り上がってきました。
③の記述をしていたHさんを指名しました。Hさんは黒板前に出て、式を書きながら説明を始めました。
「整数のわり算なら解けるので、どっちにも×20をします。『( 3 4 ×20)÷( 2 5×20)』になって、計算すると『15÷8』になるので、 15 8です。」
ほとんどの子は曇った表情です。そこで、「もう一度、同じ内容を言える人はいますか?」と発問しました。
Iさんを指名しました。
「整数のわり算にするために、4と5の最小公倍数20をかけます。すると、『(
3
4
×20)÷(
2
5×20)=15÷8』になって、商分数で表して
15
8です。」
今回は「最小公倍数」と「商分数」いう言葉を引き出すことができました。しかし、「わり算のきまり」が出てきません。そこで、「20をかけたら、わり算の答えが変わるんじゃないかな?」とあえて誤答を投げかけました。
この「教師が誤答を言う」という手立ては、子供たちから正しい考えを引き出すのに有効です。誤答と同じ考えをもっていた子たちが矢面に立たずに考えを修正する機会を作れますし、正しい考えの子たちが、「いや、それは…」と意欲的に発表してくれます。案の定、Jさんが動き出しました。
「先生、答えは変わりませんよ。だって、小数のわり算のときも『わられる数とわる数に同じ数をかけてもわっても答えは変わらない』を使って計算しました。」
続けてKさんが付け足します。
「『わり算のきまり』と言います。」
二人の発表を聞いて、自然に拍手が起きました。
だったら…
と統合・発展を促す発問をしました。子供たちは、じっと黒板を見つめます…。
しばらくすると、Lさんがはっと気が付いた顔をしたので、指名します。
「逆数かな?Aさんの考え(①)もFさんの考え(②)も逆数が使われている。Hさんの考え(③)にも逆数があれば完璧なんだけど…」
周りの子たちも頷いています。
Mさんが「頑張れば逆数が見えるよ…」と手を挙げました。そして、黒板に下記の式を書きました。
3
4×20 =
3
4×
4
3×15
2
5×20 =
2
5×
5
2×8
これを見て、大きな拍手が起きました。どの考え方にも「逆数」が関係していることを子供たちが見出すことができました。
次回は、5年「小数のかけ算」を取り上げます。お楽しみに!


種市 芳丈(たねいち よしたけ)
小中一貫三戸学園 三戸町⽴三戸⼩学校・三戸中学校 教頭
子供たちが夢中になる算数授業づくりに取り組んでいます。算数専科や複式学級の指導の経験あります。今、チャレンジしているのは、ロイロノートを活用した算数授業です。算数の教材づくりの会「ガウスの会(代表:細水保宏)」の会員。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
