既習を生かして「なるほど！」を作り出す３＜５年：小数のかけ算＞ 「はてな？」「なるほど！」「だったら…」で作る算数授業（第6回）

「８０×３」は同数累加（８０＋８０＋８０）で式を意味付けることができますが、かける数が小数になる「８０×２．３」になると同数累加で式を意味付けることが困難になります。

例えば、以下で紹介する実践でも「８０×２．３」を「８０＋８０＋０．３」と発言した子が、その直後に「…あれ？」と混乱した様子が見られました。きっと、かけられる数が２桁になっても小数になっても適用できていた「同数累加」が、かける数が小数になった途端、「．３」をどのように考えればいいのか分からなくなったと考えられます。

つまり、かける数が小数になると、かけ算の意味を見直す必要が出てきます。「かけ算の意味の拡張」とも言われます。もちろん、教える内容ですので、一方的に「８０を１と見たとき、２．３倍にあたる大きさをもとめること」と教えてしまうこともできますが、「子供からの必要感」や「その理解を促す図」がある場面にしたいものです。

このようなことから、私も「小数のかけ算」の指導で悩んでいました。そんな中、『少なく教えて多くを学ぶ算数指導』（1997年発行・明治図書出版・絶版）を紹介していただきました。

この本は、第４回と第５回でも紹介した杉山吉茂先生（東京学芸大学名誉教授）の編著書です。２００２年度から始まる週５日制の前に、もし授業時間数が減っても内容を減らさない指導の工夫について「算数教育」に連載していたものをまとめた本です。特に参考になった内容をいくつか列挙します。

• 「比例関係」「（比例）数直線」「十進位取り記数法」「たし算のきまり」「アレイ図」「かけ算のきまり」「わり算のきまり」など、繰り返し活用される知識と具体的な事例が掲載されています。次期学習指導要領のキーワードである「中心的な概念」の参考になると思われます。
• 上記のような知識を互いに関連付けて指導をすることで、覚えたことを忘れにくくするたけでなく、それらを活用して算数を作り出す指導ができることを示唆しています。現在行われている「主体的・対話的で深い学び」にもつながります。
• 「小数のかけ算」「小数のわり算」「分数のかけ算」「分数のわり算」の事例を掲載されています、教科書だけでは分かりにくい比例数直線を使った指導の意図やその指導の仕方が分かります。

なお、この本も前回紹介した「復刊投票」に挙げられています。現在あと１９票で復刊となっています。

今回紹介する「小数のかけ算」の実践は、前述の本を参考にして次の３つの工夫をしています。

1. かける数の小数を強調する提示
   まず、「８０×３」になる問題文を提示し立式させます。その後、小数「２．３」に置き換えます。このことで、かける数が小数になったことを意識したり、「８０×３」から類推して「８０×２．３」を立式したりする姿を引き出します。
2. 実際の大きさを提示し理解を促す
   児童がまだ比例数直線に慣れていない実態から、実際の長さのテープ図を示し、「３ｍ」や「２．３ｍ」の示しながら、比例数直線をイメージさせていきます。かけ算の意味を見直したり、ｍではなく㎝で考える計算の仕方を考えたりするアイディアを引き出しやすくします。
3. 「かけ算のきまり」の強調
   繰り返し出てくる知識「かけ算のきまり」が活用できた場合は、そのことを褒め、板書に残して強調し、顕在化する指導します。振り返った時に、子供自身で気付けるようにします。

立式と計算の仕方に分けて２時間で授業を行いました。前時は立式場面です。（板書の写真参照）

はじめに「１ｍのねだんが８０円のリボンを３ｍ買いました。代金はいくらですか？」という問題の立式（８０×３）をしました。黒板の幅をいっぱいを使ってテープ図を意識した比例数直線を示し、式の意味は「８０＋８０＋８０」であることを確認しました。

次に、「あ！問題を書き間違えた…」と言って、「３」を「２．３」に変更しました。
すると、子供たちから次のような声が聞こえてきました。
「あ！小数になった…」
「（かける数が小数だから）かける数で表せない…」
「工夫すればいいかも…」
などの戸惑う反応が見られました。

次に、自力解決の時間をとり、ノートに式を書かせました。机間巡視をすると、「８０×２．３」「２．３×８０」「８×２３」「８×2310」の考えがありました。そこで、それぞれの考えを共有していきました。

＜８０×２．３＞

＜２．３×８０＞

＜８×２３＞

＜８× 23 10＞

みんなの考えを共有した結果、かける数に小数を使いたいけど、かけ算の式の意味を考えるとしっくりこないことが明らかになりました。

そこで、かける数が小数になってもいいように、かけ算の意味を少し変えたらどうだろうと提案してみました。
「え！そんなことしていいんですか？」
「今までのかけ算の意味はどうなるんですか？」
と子供たちは不安そうです。

「今日はまだ出ていませんでしたが、かけ算の意味に『倍』の意味もありましたね。それを使ってかけ算の意味を次のように約束し直します。『８０を１と見たとき、２．３にあたる大きさを求める』としたらどうでしょう。」と教え、そのことを黒板に言葉と図で板書していると、

「『８０×３』は、８０を１と見たとき３にあたる大きさ…」
「『８０×２』だったら、８０を１と見たとき２にあたる大きさ…」
などのつぶやく声が聞こえてきました。

大人もそうですが、新しい概念や知識を理解するには、今までの概念や知識と関連付ける作業が必要です。子供たちも同様で、このつぶやきは必死に理解しようとしている姿だと思いました。

しばらくすると、
「よし！すっきりした。」
「え、まだ少しもやっとするけど、黒板の図を見ると、これでいけると思う。」
などの声が聞こえてきました。

さらに、Ａさんは、
「かける数は小数でいいのは分かったけど、計算はどうやるんだろう？」
と次時につながるつぶやきを言っていました。

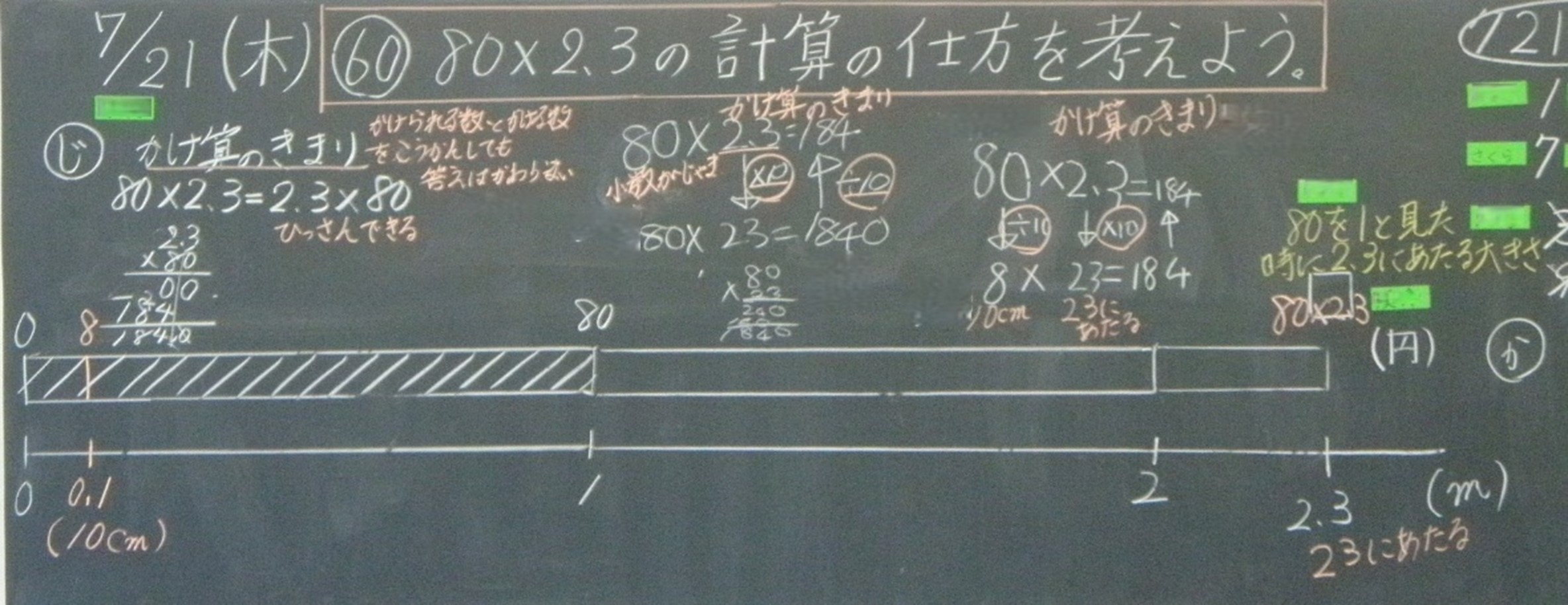
次時は計算の仕方の場面です。（板書の写真参照）

まず、前回、Ａさんが「かける数は小数でいいのは分かったけど、計算はどうやるんだろう？」と考えたことを紹介しました。

すると、子供たちは、
「かけ算のきまりを使えばいいんじゃないかな？」
「前回の『２．３×８０』が使えそう…」
「『８×２３』も使えるんじゃない？」
と次々に見通しをたて始めました。

この学級は自ら見通しを立てる子が多いため、普段から見通しを立てる発問はしていません。逆に、そんな発問をしたら、「自分で考えたかったのに…」と苦情が出るでしょう。でも、学級によっては、見通しを立てる発問をしまいまま自力解決させると、何もできないで終わってしまう子が多いこともあります。そのようなことが予想される場合は「今まで似た問題はなかったかな？」「習ったことで解決に使えるものはないかな？」「簡単な数に置き換えられないかな？」「答えはいくつになりそうかな？」などの発問で見通しを立てさせるとよいでしょう。

次に、自力解決の時間をとり、ノートに考えを書かせました。机間巡視をすると、以下の３つあったので、それぞれの考えを共有していきました。

＜Ｂさん…２．３×８０＞

• かけられる数とかける数を反対にしても、答えは変わらない。
• 小数×整数は習っている。
• ２．３×８０＝１８４

＜Ｃさん…８０×２３＞

• 小数がじゃまなので２．３を１０倍して、８０×２３
• ８０×２３＝１８４０
• １８４０は１０倍した数なので１０で割って答えは１８４

＜Ｄさん…８×２３＞

• ８０を１０で割って２．３を１０倍すると、８×２３
• ８×２３＝１８４
• １０cmで考えると、「１０cmで８円のリボンを２３こ分買った値段」を求めることと同じ。

どの考えでも、１８４になったことで、みんなで笑顔になりました。子供たちに３人の考えの中で共通しているものはないかを考えさせました。

すると、Ｅさんが
「ＣさんとＤさんは、かけ算のきまりを使っています。」
と発表しました。

みんなで、黒板の書かれたＣさんとＤさんの考えを見直しました。

かけ算のきまりを使った分かるところを声に出し、オレンジ色で囲んでいきます。
「Ｃさんは『↓×１０』と『↑÷１０』、Ｄさんは『↓÷１０』と『↓×１０』。」

Ｅさんの話がよく分からずじっと黒板を見ていた数人も、途中から一緒に声を出しました。次に、振り返りを書かせました。いつもより早めに取り組ませたのは、前時と本時の２時間分を振り返るためです。

なかなか進まない子のために、前時の板書を電子黒板に映しておきました。

７分後、いいなと思った子の記述を発表させました。

「小数のかけ算で、かけ算の意味が広がってびっくりしました。もしかして分数のかけ算でも広がるかもしれません。また、かけ算のきまりがこんなに便利だとは知りませんでした。」
「先生が黒板のかいた図が、とても大きくてびっくりしました。でも、わざわざかいた意味が分かりました。図があると、ヒントになるからです。次からは、わたしも図をかいて問題をとくようにします。」
「今までかけられる数やかける数が小数でも気にしていませんでした。でも、かけ算の意味が変わるくらい違うことが分かりました。次は筆算だと思うけど、やり方は変わるのかな？」

次時は、最後の子の振り返りから、小数のかけ算の筆算のやり方に入れそうです。

次回は、３年「かけ算のひっ算」を取り上げます。お楽しみに！