子どもは正しく間違える?
ー算数のつまずきからわかる子どもの理屈の認知科学ー(後編)
ABLE ONLINE #05リポート

認知科学の視点から学習研究と教育実践をつなぐ国際コミュニティABLE(Agents for Bridging Learning research and Educational practice)のオンラインセミナーABLE ONLINE #05「子どもは正しく間違える? ー算数のつまずきからわかる子どもの理屈の認知科学ー」。前編では、認知科学者の今井むつみ氏と、数学者の谷口隆氏の講演の模様をリポートした。後編では、言語学者の広瀬友紀氏の講演と、パネルディスカッションをリポートする。
数字とことばの意外な関係

東京大学 総合文化研究科教授 広瀬 友紀 氏
続いて、心理言語学を専門とする言語学者の広瀬友紀氏が登壇。算数に関わる言葉由来の難しさについて、事例を挙げて解説した。
数式と言語は階層構造が生み出す構造的多義性があるという点で共通しているが、それをどう扱うかという点において、学校で扱う数式と普段の言語使用には大きな違いがあるという。
学校では、かけ算、わり算はたし算、ひき算より先に計算する、カッコでくくられた部分は先に計算する、それ以外は左から先に計算する、という決まりを教わる。この「左から先に」というのは、人間が便宜上、多義性を避けるために作ったものであり、宇宙の法則ではないが、それに従うことで解が1つに絞られる。例えば18−10+5は(18−10)+ 5 =13 と計算するのが正解で、18−(10+5)= 3とすると不正解になる。
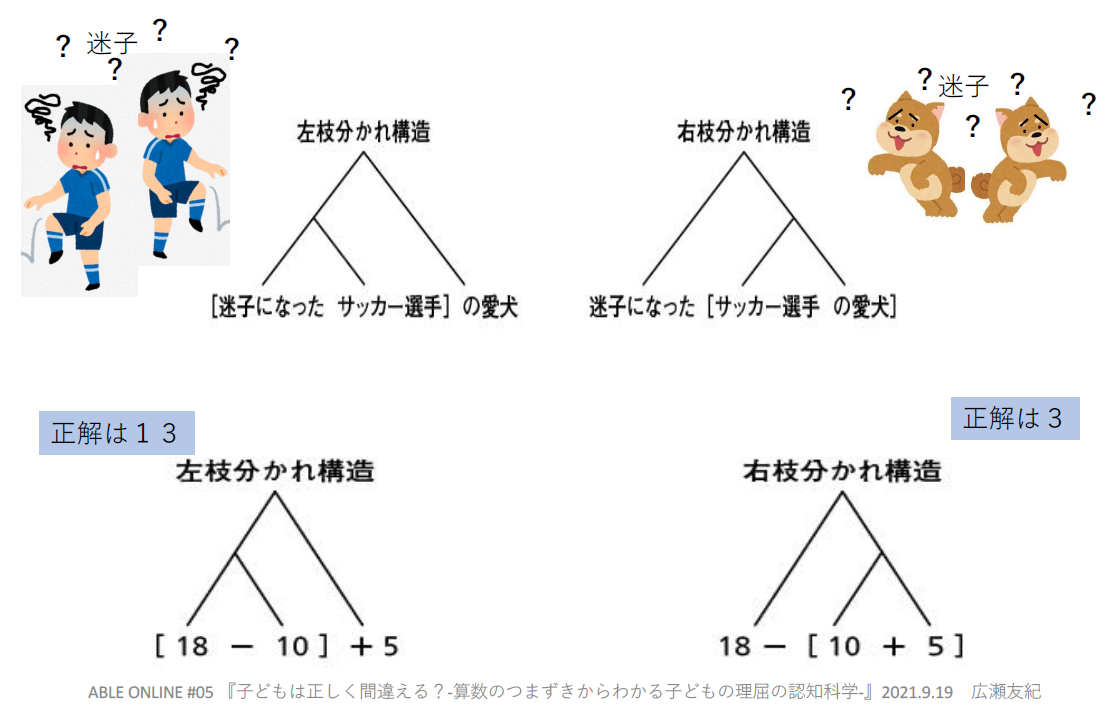
一方、言語においてはそのような決まりはない。広瀬氏は「迷子になった選手の愛犬 拡散に次ぐ拡散、最後には発見」というニュース記事の「迷子になった選手の愛犬」という表現を例にとり、その階層構造を説明した。「迷子になった」「選手」「愛犬」というように要素が3つあると、左側の2つを先にまとめる「左枝分かれ構造」と右側の2つを先にまとめる「右枝分かれ構造」という2通りの考え方が生じ、どちらを選ぶかによって異なった解釈が生み出される。
これは先ほどの数式にもあてはまり、左枝分かれ構造の(18−10)+ 5 で計算すると正解は13、右枝分かれ構造の18−(10+5)で計算すると正解は3と、2通りの答えが生じうる。
「言語の場合、例えばこの例では、私たちは意味や常識を駆使したり、事前情報などの文脈を使ったりして、結果的に『選手の愛犬が迷子になった』という右枝分かれ構造を支持します。"左から順に"解釈すれば『迷子になった選手に愛犬がいる』という左枝分かれ構造が得られますが、ここではその選択はしないのです。数式の場合は、先に述べた決まりによって正解を決めているわけですが、子どもはこの決まりを実行するところでつまずくことがあります。しかし、本来複数の解がありうるということを理解しているという点においては、より真実に近いところにいるという見方もできるでしょう」(広瀬氏)
また、広瀬氏は「かける数」「かけられる数」という、子どもだけでなく大人も間違いやすい表現についても言及した。これには⽇本語の関係節(名詞を修飾する節)に特有の曖昧性がかかわっており、そもそもつまずきやすくできているのだという。
例えば、「5に3をかける」というのは5を3倍することであり、5がかけられる数(被乗数)、3がかける数(乗数)となる。この「5に3をかける」を関係節で表現すると、助詞の「を」が脱落して「5にかける3」、あるいは「に」が脱落して「3をかける5」となる。さらに、日本語では⽬的語の省略も可能なので、「(5に)かける3」とも「(3を)かける5」とも言えてしまう。受け身の「3が5にかけられる」を関係節で表した場合も同様で、「(5に)かけられる3」とも「(3が)かけられる5」とも表現することが可能になる。
自然言語の場合、私たちは文脈を駆使することで意味を理解しているが、数には文脈がない。そのため、「かける数」「かけられる数」の理解は難しいのである。
「よく算数ができないのは読解⼒や国語力の問題だと言われますが、逆に、こうした日本語の性質に敏感に気づいている子どもの方が混乱しやすく、『正しく間違えている』と言えるケースや、正しいのに間違いにされてしまっているケースが発生しているかもしれません。むしろ『かける数』『かけられる数』の表現については、⼤⼈が子どもに先回りできるだけの国語⼒を要求されているとも言えるでしょう」(広瀬氏)
子どもの間違いに気づき、その理由を考える習慣を
「福山100NEN教育」の今年度のテーマ
最後に、岩波書店の自然科学書編集部編集長、濱門麻美子氏がモデレーターを務め、今井・谷口・広瀬の3氏と、元中学校教員で、今井氏の調査に協力した広島県福山市教育委員会の教育長、三好雅章氏によるパネルディスカッションが行われた。福山市では、認知の仕組みから学習方法を見直すことに取り組み、子ども達が「使える知識」を身につけられるような学びを追求しているそうである。
「今までわからないという児童に、絵や数直線に描いてごらんと言っていましたが、自分は何度も使った経験があって使いこなしているものだけれど、子どもにはわかりやすくないのだと気づかされました」という小学校教員の参加者の感想が紹介された。これに対し、今井氏は「今回の調査で、1は1個や1cmと考えていて、描いた数直線を定規で測ろうとする子も多く、1というものを相対化して考えることは小学生にとっては難しいということが再確認された」と補足した。
三好氏は、3氏の講演で紹介されたような子どものつまずきが日々、教育現場で起こっているとして、「抽象化すると難しいからと、具体物で説明するとそれにずっと引っ張られてしまい、混乱している子どもも多い。そのような事例を教員間で共有し、授業実践に活かしていくにはどうすればよいか」と疑問を投げかけた。この発言を受けて、チャットに「子どもが規則的に間違えるのであれば、そのパターンを網羅的にリストアップできないか」という提案が投稿された。
左上:(株)岩波書店 編集局 自然科学書編集部編集長 濱門 麻美子 氏
左下:福山市教育委員会 教育長 三好 雅章 氏
これに対し、今井氏は「以前から構想はあるものの、なかなか実現できていないが、子どもの間違いの事例を現場の教員や保護者などから収集するウェブサイトを作り、それを研究者が分析・解説して、間違いを体系的にまとめるとよいのではないか。算数だとハードルが高ければ、言葉の間違いでもたくさんあるし、面白いのではないか」と提案。セミナー参加者のチャットには実現を望む声が多数寄せられ、広瀬氏も「そうした間違いについての知見が頭の中に蓄積されていると、授業の中で子どものつまずきを敏感にキャッチしたり、短い時間で対処したりすることが可能になるかもしれない」とコメントした。谷口氏は、子どもの間違い方は実に多様であるため、網羅しすぎると逆に参照しにくくなる可能性もあるとして、「典型的な間違いに絞るとよいのではないか」と意見を述べた。
とはいえ、教員や保護者が、子どもの間違いに気づいた時に体系を眺めても、何につまずいているのかがすぐには理解できない可能性がある。今井氏は、「間違いの体系は非常に参考になるとは思いますが、それに頼りきらずに目の前の子どもを見つめ、この間違いはどこから来ているのか、なぜここが難しいのか、と考える習慣を付け、熟達していくことが大事だと思います」と訴えかけた。
記者の目
子どもの間違いには必ず子どもなりの理屈があり、間違いの中にも正しさが含まれている。このことを明確に示した今井・谷口・広瀬3氏の講演は、多くの気づきに満ちていた。ここで得た気づきを授業実践に活かしていくためにも、子どもの間違いを体系的にまとめたウェブサイトの実現が期待される。また、子どもがスキーマを獲得したり、誤ったスキーマを修正したりできるようにするために大人ができる支援として、日常生活の中で子どもと算数を楽しむ谷口氏の実践は大いに参考になると感じた。
関連記事
参考
取材・文・画像:学びの場.com編集部
※当記事のすべてのコンテンツ(文・画像等)の無断使用を禁じます。
ご意見・ご要望、お待ちしています!
この記事に対する皆様のご意見、ご要望をお寄せください。今後の記事制作の参考にさせていただきます。(なお個別・個人的なご質問・ご相談等に関してはお受けいたしかねます。)
この記事に関連するおススメ記事

「教育リポート」の最新記事














 授業実践リポート
授業実践リポート 食育と授業
食育と授業 教育リサーチ
教育リサーチ



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事 ご意見・ご要望
ご意見・ご要望