和差算

48cmのリボンを切って、A、Bの2本に分けます。AはBよりも8cmだけ長くなるようにするためには、AとBをそれぞれ何cmにすればよいでしょうか。
解法を見る



ある真分数の分母と分子の差は14で、分母と分子の和は98です。この分数を求めて約分しなさい。
解法を見る



長さ30ｍのロープを切って、Ａ、Ｂ、Ｃの３本に分けました。ＡはＢより5ｍ長く、ＢはＣより2ｍ長くなっています。このときＡ、Ｂ、Ｃそれぞれの長さを求めなさい。
解法を見る

48cmのリボンを切って、A、Bの2本に分けます。AはBよりも8cmだけ長くなるようにするためには、AとBをそれぞれ何cmにすればよいでしょうか。

■ 解法
和差算の基本問題です。和差算の問題は次の3つの解き方で解くことができます。

解法(1)：図に表して解く

解法(2)：公式で解く

解法(3)：方程式で解く

では、それぞれの方法で解いてみましょう。

解法(1)：図に表して解く



和（合計）は48cmですから、仮にAのリボンの8cm分をのぞいた場合、残りはcmのリボン2つ分（Bのリボン2本分）になります。このcmのリボン2つ分長さは、48－8＝40cmであり、cmリボン1本分の長さ（Bのリボンの長さ）は20cmであることがわかります。
よって、Aのリボンは20＋8＝28cm、Bのリボンは20cmにすればよいことがわかります。

■ 答え
Aのリボンは28cm、Bのリボンは20cm

このように問題文だけを見て、頭のなかだけで考えると、混乱しそうな問題も、図に表すと簡単に解けてしまうことがわかると思います。問題文を図で表すことができれば、問題は解けたも同然です。


解法(2)：公式で解く
和差算の公式は次の通りです。とてもよく知られている公式です。

ここでは、2つのリボンの長さの和は48cm、差は8cmですから、この公式にあてはめてみると、
大きい方の数＝（和＋差）÷２＝（48＋8）÷2＝56÷2＝28　　…Aのリボン
小さい方の数＝（和－差）÷２＝（48－8）÷2＝40÷2＝20　　…Bのリボン
と簡単に解けてしまいます。

■ 答え
Aのリボンは28cm、Bのリボンは20cm

では、なぜこの公式で解けるのでしょうか。もう一度、図で考えてみましょう。
実は、小さい方の数は先ほどの解法(1)の考え方そのものです。
和（48cm）から差（8cm）を引くとcmリボン2つ分の長さ（40cm）になりました。
これを2で割ればcmリボン1つ分の長さ（Bのリボン）が出るわけです。つまり（和－差）÷２です。


【和－差の図】　小さい方の数＝（和－差）÷２



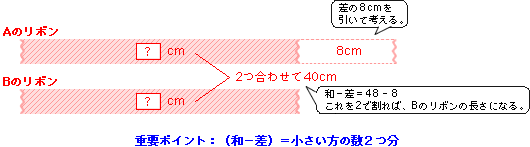
次に大きい方の数を求める公式を考えてみましょう。（和＋差）というのは、もとのリボン（48cm）に差（8cm）と同じだけのリボンを新しく用意してつなげることになります。この8cm分をBのリボンの方に加えてみましょう。するとAのリボンと同じ長さのものが2本できます。これを2で割ればAのリボンの長さ（大きい方）ということになります。つまり（和＋差）÷２です。


【和＋差の図】　大きい方の数＝（和＋差）÷２



重要ポイントについて
図を見ると分かると思いますが、
和－差を求める理由は、長さを小さい方にそろえて小さい方の数の2倍を求めるためです。
和＋差を求める理由は、長さを大きい方にそろえて大きい方の数の2倍を求めるためです。
そして、それぞれ２で割れば、小さい方の数と大きい方の数が出てくるわけです。
この「長さをそろえる」という考え方は、和差算の応用問題を解くときの大切なカギとなります。


解法(3)：方程式で解く

Aのリボンの長さをχとすると、Bのリボンの長さは χ －8となります。和は48cmですから、



■ 答え
Aのリボンは28cm、Bのリボンは20cm

※ 和差算は通常小学校3年生で習い、算数なので方程式は使いません。
そのため以下の問題ではこの解法(3)は割愛させていただきます。

ある真分数の分母と分子の差は14で、分母と分子の和は98です。この分数を求めて約分しなさい。

■ 解法
これも和と差がわかっているので、和差算の問題です。真分数なので、分母が（大きい方の数）、分子が（小さい方の数）になります。

解法(1)：図に表して解く



和が98で差が14なので、分子２つ分の大きさは
98－14＝84
したがって分子は
84÷2＝42
分母はそれより14大きいので
42＋14＝56
よって、求める分数は



■ 答え


※ここでは小さい方の分子に長さをそろえて解いたことになります。


解法(2)：公式で解く




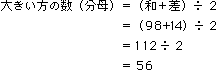
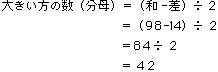
よって、求める分数は




■ 答え

長さ30ｍのロープを切って、Ａ、Ｂ、Ｃの３本に分けました。ＡはＢより5ｍ長く、ＢはＣより2ｍ長くなっています。このときＡ、Ｂ、Ｃそれぞれの長さを求めなさい。

■ 解法
和差算の応用問題です。いままでのように２つに分けるのではなく、ここでは３つに分けています。どうやって求めればよいのでしょうか。ヒントは問題１の解法(2)で説明した重要ポイントにあります。「長さをそろえる」という考え方をすれば、２つに分ける場合でも、３つに分ける場合でも同様にして解くことができます。それでは、まず図に表してみましょう。



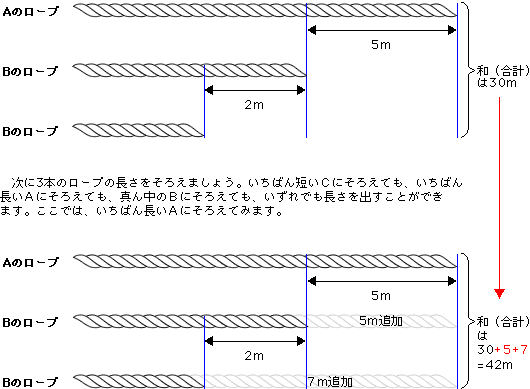
このように、Ｂのロープに5ｍ、Ｃのロープに7ｍ追加すると、3つのロープの長さがそろいます。これで、Ａのロープ3本分になりました。

Ａのロープ3本分で、30＋5＋7＝42ｍ　だから、
Ａのロープの長さは42÷3＝14ｍ
Ｂのロープの長さは14－5＝9ｍ （Ａよりも5ｍ短いから）
Ｃのロープの長さは9－2＝7ｍ （Ｂよりも2ｍ短いから）


■ 答え
Ａは14ｍ、Ｂは9ｍ、Ｃは7ｍ