学びに向かう力、人間性を育む算数教育（前編） ―北区立王子第五小学校 算数科・研究発表会リポートー

北区立王子第五小学校は「学びに向かう力、人間性を育む算数教育」を目指し、「自立」「協働」「創造」「学習における自己調整」という4つの力を育成する「王五小自律的探究モデル」を設定している。

【自立】試行錯誤しながら粘り強く取り組む
【協働】思いやり・優しさをもち、違いを認め、共に学ぶ
【創造】価値ある新たなものを求め、創り出す
【学習における自己調整】振り返り、自己調整しながら探究する

前編では、4つの力の中でも「協働」に比重を置いた4年生の授業をリポートする。「思いやり・優しさをもち、違いを認め、共に学ぶ」ために授業者がどんな工夫をしているのか、考えながら読み進めてほしい。

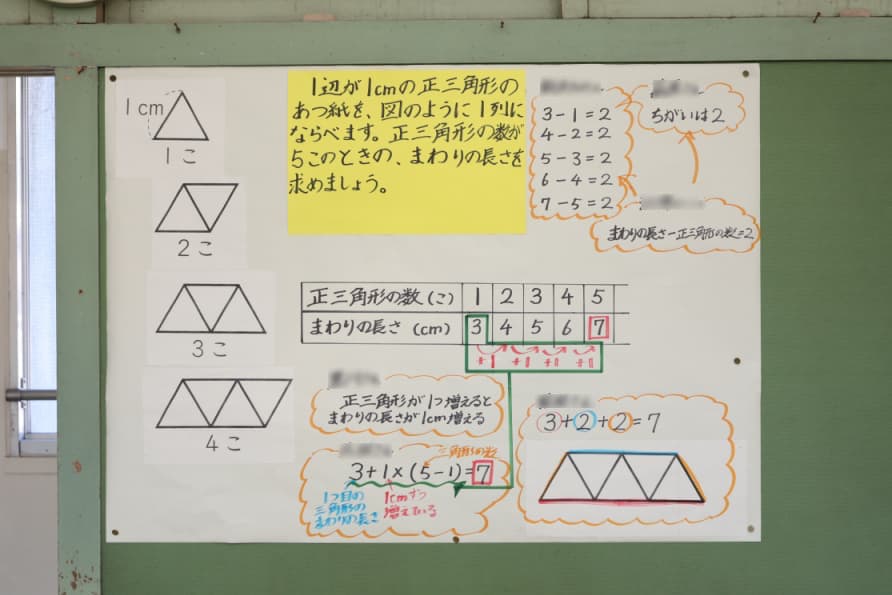
前時の授業では、1辺が1cmの正三角形を階段状に並べた時の段の数と、周りの長さの関係を、図や表、式を使って調べた。

授業の冒頭で、市野教諭は次のように呼びかけた。

「前回と同じように、友だちの考えのいいところを探してほしいなと思います」

本時の問題は、「テーブルが5個の時、いすの数は何個ですか」。

まずは自分の考えをもつため、市野教諭は答えの求め方をノートに書くよう指示。児童たちは図や表、式を使って各々の方法で答えを求めていた。

ノートに書いた答えを伝え合う。まずは表を使った児童が自分の考えを発表。

「テーブルの数が1個の時いすは5個で、テーブルの数が2個の時はいすが8個、テーブルの数が3個の時はいすが11個、テーブルの数が4個の時はいすが14個、テーブルの数が5個の時はいすが17個」

「17ってどうやって求めたの？」という市野教諭の問いに対し、別の児童が「元々いすの数が5個あって、＋3ずつ増えていって17になる」と回答した。

次に市野教諭が「式が書けた人はいる？」と問いかけると、3人の児童が以下の3つの式をあげた。

Aさん「3×5＋2=17」

Bさん「5＋3×(5−1)＝17」

Cさん「5＋4＋2×(5-1) ＝17」

Bさんの式（「5＋3×(5−1)＝17」）について

3人の式が何を表しているのかそれぞれノートに書いた後、「まずはBさんの式（「5＋3×(5−1)＝17」）が分かる人？」と市野教諭が問いかけると、ひとりの児童が以下のように説明した。

「多分、3×4が12ってところは3の数が4個で、ここにある4つの3をまず計算して、残った5を足したんじゃないか」

Bさん本人も自分の考えを説明。

「テーブルが1つの時のいすの数が5個で、＋3は4個ある」

その後、隣同士でBさんの考えを説明し合う。児童たちは「なるほど、そういうことか」と言いながら、Bさんの考えについて理解を深めていた。

隣同士で説明し合った結果、Bさんは「表」を使って式をつくったことに多くの児童が気付く。市野教諭は、この気付きをノートに書いておくよう指示した。

Aさんの式（「3×5＋2=17」）について

ひとりの児童が、「まず（ひとつの台形に対していすが）3個あって、テーブルが5個あるから、3の部分を全部あわせて3×5にして、残った（台形の横の部分の）2つの2を足して17」と図を使って説明。多くの児童がこの説明に納得したようだった。

この回答に加え、Aさん本人は以下の考えを付け加えた。

「横の2つは（テーブルの数が）いくつになっても2つだと思うから、後で足した」

Aさんの式についても、隣同士で説明し合った後、気付いたことをノートに書いていく。Bさんが「表」を使って式をつくったのに対し、Aさんは「図」を使って式をつくったことに多くの児童が気付いていた様子だった。

Cさんの式「5＋4＋2×(5-1) ＝17」について

次はCさんの式（「5＋4＋2×(5-1) ＝17」）について皆で考えていく。当初、テーブルといすの数の差に着目したCさんの式には多くの児童が苦戦している様子だった。

ひとりの児童が、「（テーブルが1個でいすが5個の時）5−1で4。（テーブルの数が2の時）8-2で6。（テーブルが3個でいすが11個の時）11-3は8。全部2ずつ上がっている。分かるのはここまで」と説明。

その後、Aさん本人が自分の考えを以下のように説明した。

「いすの数とテーブルの数の差が＋2になっている。（テーブルが1個の時の）5は置いておいて、＋4は（テーブルが1個の時、いすの数が5なので、その差の）4で、（5-1）は（表の）間の数　」

その後市野教諭は、あえて不安そうな顔をしている児童に問いかける。

「多分でも説明してみて。わからないところはCさんが助けてくれるから」

Cさんの式を理解した児童が増えてきたところで、隣同士で説明し合い、気付いたことをノートに記入。友だちと学び合うことで、少しずつ理解していく児童の姿が印象的だった。

授業が終わる10分前、市野教諭は本時のテーマ「いつでも使える式ってどんな式？」にまつわる問いを投げかけた。

「どの式もいいなと先生は思うんですけど、テーブルが何個でも使える式ってどんな式？」

この問に対し、ひとりの児童が「◯、□で考える」と回答。そこで、テーブルを□、いすを◯で表すことにし、各々が答えをノートに書いていった。

Bさんの式は「5＋3×（□―1）＝◯」、Aさんの式は「3×□＋2＝◯」と答えられる一方、Cさんの式はなかなか答えにたどり着かない。時間切れとなり、Cさんの式を◯□で表せるかどうかは次時への持越しとなった。

授業の最後、本時の授業に対し、以下のような気付きがあったと児童たちから声があがった。

市野教諭は以下の言葉で授業を締めくくった。

「自分の考えだけじゃなく、友だちがどう考えたのかについても、ノートにたくさん書いてみてください。また、最初自分がわからなかった場合は、友だちの考えに触れることで、どこからわかるようになったのかも書いてみましょう。学びの手ごたえがあるはずです」