構造のしくみ(vol.2) 面の構造~サンドイッチ、ハニカム、ドーム、アーチ構造~

みなさんこんにちは。今回も、前回に引き続き、建物やものの構造の不思議について一緒に考えていきましょう。みなさんは海外旅行をしたことがありますか? 海外旅行は飛行機のおかげでとても身近なものになりました。飛行機はとても大きなものですが、なぜ安全に飛ぶことができるのでしょうか。ここには、様々な構造の不思議が隠されているんですよ。
1飛行機の壁の構造(1)平面板と芯材で作るサンドイッチ構造
高い空では空気は薄いため飛行機の外は気圧が低いのに対し、機内では人が快適に過ごせるように地上と同じくらい気圧を高く保っています。内外の気圧の差によって機体の壁にはとても大きな力が加わり、しかも壁は広いので大きな力に耐えるためには厚い壁が必要になります。でも厚い壁では重くて飛ぶことができなくなってしまいます。
軽くて壊れにくい壁をつくるには、どのような構造でつくればよいでしょうか?
|
次の中で軽いわりには壊れにくい構造のものはなんですか?
|
B の段ボール箱
ダンボールは、2枚の厚紙の間に波型の紙の芯がサンドイッチ状に入っていています。このために軽いのに丈夫で、とても重い物を入れても壊れずに運べるのです
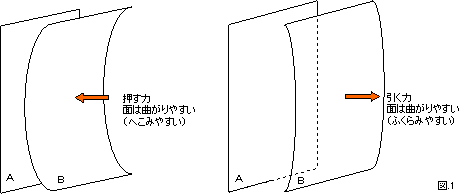
図1 A平面は固定でB平面に力を加える。2枚の板の間に物(芯材)がはいっていないとき、面はまがりやすい。
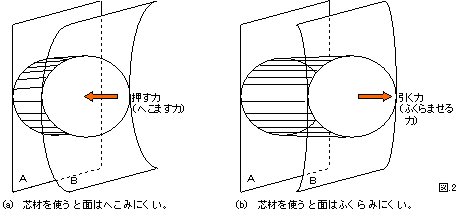
図2 サンドイッチ構造。
2枚の板の間に芯材として円筒を入れた構造
2枚の板の間に筒(芯)を挟んでみます。平面を曲げる力は筒の伸び縮みの力に変わります(図2、図3)。平面は曲がりやすいけれども、筒は伸び縮みしにくいので、板は変形しにくくなります。2枚の広い板の間に芯を入れて変形しにくくしたものをサンドイッチ構造といいます。飛行機の壁の構造には、実はサンドイッチ構造が使われているのです。
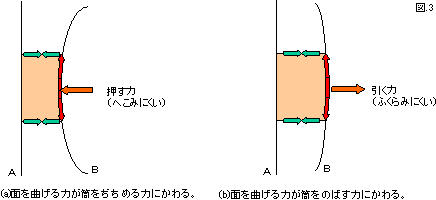
図3 加わる力の変化。図2の絵を横から見たところ。
|
![]()
軽くて壊れにくい面の構造はどのように作ればよいか理解する。それらが日常の生活のなかでどのように使われているのか考察する。ひとつの構造物を追加することによって、強度の違いが出てくることを理解する。
![]()
身の回りのサンドイッチ構造を探してみましょう。また、飛行機のどの部分にサンドイッチ構造が使われているか調べてみましょう。
2飛行機の壁の構造(2)ハニカム構造
蜂の巣のことを英語でハニカム(Honeycomb)と言います。この蜂の巣のかたちによく似た「ハニカム構造」について、ここから一緒に考えていこうと思います。
|
では、ここでクイズです。「ハニカム構造」の断面は、どんな形をしているでしょうか? 次のうちのどれか選択してください。 |
A 正六角形
蜂の巣は不思議な形をしています。たくさんの筒が平行に隣り合ってくっつきあい、一つの巣を作っています。一つ一つを見てみると、断面が六角形をしています。筒をたくさん並べて作るハニカム構造でも、筒の形として正六角形がよく使われます。それはどうしてでしょうか?
3飛行機の壁の構造(3)ハニカムの筒の形
ハニカムの筒はなぜ正六角形なのでしょうか? ひとつひとつの筒の中の空間を最も広くでき、筒を作る壁の材料が少ないのは正六角形です(図4(d))。もし壁の材料が同じ量だったら、一番広い面積をつくるには正六角形が一番効率の良いことになります。より少ない材料で広い空間を覆うことができるということは、「より軽く」なるのです。だから正六角形がよく使われるのです。
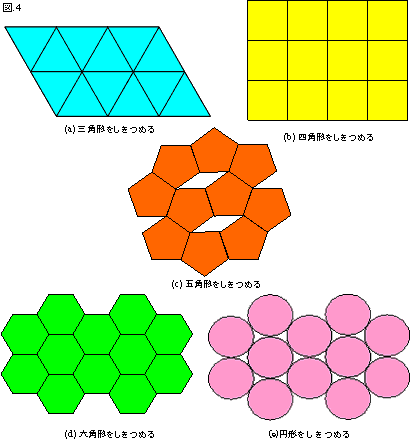
図4 平面を同じ大きさの正多角形で敷き詰める方法
正三角形、正四角形、正六角形では、すきまなく敷き詰めることができる。
正五角形、円形では平面を完全に覆うことができず、かならずどこかにすき間ができる。
ハニカムとは蜂の巣のことでたくさんの筒が平行に並んでいることはわかったよね? 蜂は、この中に蜂蜜を蓄えたり、中でミツバチの子どもを育てたりしています(図5)。筒の壁は蜂が生産したミツロウでできています。でも飛行機ではロウではなくて、アルミニウムなどの軽い金属板を使います。これを芯材としてサンドイッチ構造に使うと軽いのに広い空間がとれ、しかも離着陸などの際に激しい力を繰り返し受けても壊れずに安全な飛行機を作ることができます。
また、芯材がハニカム構造だとたくさんの筒の一部が壊れてもその破壊力が他の筒に及びにくいので平板の一部の傷が飛行機全体の破壊を引き起こしません。この点でもとても有利な構造です。
ところで、ハニカム構造も、サンドイッチ構造も、柱や板の曲げる力を芯材の伸び縮みに変えることによって軽いのに強いという特徴があります。これは、前回お話したトラス構造と同じ考え方なんですよ。
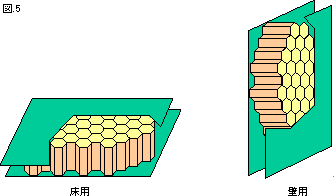
図5 ハニカム構造の芯材を使ったサンドイッチ
|
![]()
丈夫な構造の飛行機ではたくさんの筒を並べたハニカム構造の芯材を二枚の平面板の間に使い、板の面に加わる曲げる(へこませる、ふくらませる)力をハニカムの筒の壁の伸び縮みの力に変えて変形を小さくします。これがハニカム材を使ったサンドイッチ構造でした。柱や板の曲げる力を材料の伸び縮みに変えることから、トラス構造とハニカム構造は考え方が同じであることを学ぶ。
![]()
![]() みなさんも身の回りにあるハニカム構造を探してみましょう。最近では、机の板やいすの座面によく使われています。壊れている机や椅子を見つけたら中をのぞいてみてください。また、ダンボールにも使われていることがあります。
みなさんも身の回りにあるハニカム構造を探してみましょう。最近では、机の板やいすの座面によく使われています。壊れている机や椅子を見つけたら中をのぞいてみてください。また、ダンボールにも使われていることがあります。
| 蜂はどうして六角形を作ることができるのだろう? ものさしで図りながら作るわけではないので、もっと別の原理がはたらくに違いない。蜂の巣はミツバチの体に合わせてたくさんの筒を作っていくとき、空間に隙間がないように、また空間が最も広くなるように詰めていくと、それが自然に六角形になってしまう結果だと考えられる。そして六角形の筒が最も軽く少ない材料で広い空間を確保できるので、蜜を貯めたり、育てたりするための巣の重さが軽くて丈夫な構造の答えとなっているのだろう。 |
4その他よく見られる構造(1)ドーム構造

図6 ギリシャ・サントリーニ島の教会
おわん型の屋根はドーム構造と呼ばれます。なぜ、屋根の部分は石が落っこちないで積み上げることがでるのでしょうか? ドームの石材1個を見ると(図8)、石材の重力Gは石材を縮める力G1と石材を曲げる力G2に変わります。これをG1成分とG2成分とよぶことにします。屋根のどこでも曲げる力G2は重力Gより小さくなり、残りの力は石材を縮める力G1になります。さらに、ドームの下の方では、屋根の重力Gはそのほとんどが材料を縮める力G1成分に変わります。石材を曲げる力G2はほとんどなくなります。つまり、屋根の面全体で、半球の面に沿って外側に広がろうとする力に変えられます。
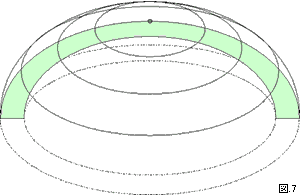
図7 ドーム屋根の透視図 ドームの中心を通る断面の図を緑色で示している。
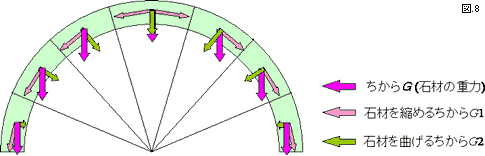
図8 ドームに加わる重力が曲げる力と縮める力に変わるようす。
G1は面に沿う重力の成分で、これが材料を縮める力として働く。
G2は面と垂直な重力の成分で、これが材料を曲げる力として働く。
曲げる力G2はもとの重力Gより小さくなる。
しかし、ドームの頂上付近ではちょっとだけ状況が違います。ここでは屋根の重力Gの一部だけが周りの石材を押す力G1に変わり、残りの成分G2は頂上付近の石材を曲げる力として残ります。しかし、頂上付近は面積も小さく石材の量も少ないので、その部分を補強すれば全体として丈夫な屋根を作ることができます。
ドーム構造では垂直方向の重力に耐えられるだけでなく、地震、風圧などの横方向の力に対しても強く、また、局部的にかかる力が平面全体に広がるためにとても大きな力にも耐えることができるんですよ! この構造のおかげで、教会などのような大きな空間をつくることができるのです。
5その他よく見られる構造(2)アーチ構造 - 丈夫な橋の構造 -

図9 ローマ時代の水道橋(スペイン)。
上の図はスペインのセゴビア市にあるローマ時代の水道橋で、石を組んでアーチ型に作られています。上に設けられた水路を通して、遠い山から市中に水を運んでいました。
今回、見てきたサンドイッチ構造、ハニカム構造やドーム構造、アーチ構造などはとても簡単な構造物ばかりです。今回の壁(面)の構造も、トラス構造と同様に材料を曲げる力を伸縮の力に変えることで丈夫な構造をつくっています。これは骨組みと面の構造で共通の仕組みだということがわかりました。最新の飛行機や、大きな大きな建物も、簡単な原理から出来上がっていることがわかりましたね。
|
![]()
少ない材料や重い材料で丈夫なものを作るには構造に工夫することを学ぶ。ひとつの構造が応用されて、様々な構造を作り上げていることを学ぶ(ドーム、アーチ構造)。歴史的に残っている各地の建造物なども、簡単な原理によって成り立っていることを学ぶ。
![]()
![]() 身近なアーチ構造の建造物を探してみましょう。アーチ構造が生活のなかでどのように応用されているか調べてみましょう。ドーム構造のさまざまな構造の種類を調べてみましょう。日本にあるドーム構造の建物を調べてみましょう。
身近なアーチ構造の建造物を探してみましょう。アーチ構造が生活のなかでどのように応用されているか調べてみましょう。ドーム構造のさまざまな構造の種類を調べてみましょう。日本にあるドーム構造の建物を調べてみましょう。![]() キリスト教やイスラム教の寺院のドーム構造の特徴や共通部分について調べてみましょう。
キリスト教やイスラム教の寺院のドーム構造の特徴や共通部分について調べてみましょう。
次回はエラトステネスの「地球の大きさをはかる」です☆お楽しみに~
監修:文部科学省 統計数理研究所 助教授 瀧澤由美博士(工学)
※当記事のすべてのコンテンツ(文・画像等)の無断使用を禁じます。
関連記事
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 算数の教え上手
算数の教え上手 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事