昔の算数に挑戦1<2年「かけ算(口遊)」> 「はてな?」「なるほど!」「だったら…」で作る算数授業(第10回)
今回は昔の乗法九九の教材です。前の連載第32回では教材だけの紹介でしたが、今回は教材研究と授業実践を加えて、詳しく紹介します。
児童自ら交換法則に気付き、それを生かそうとする姿を育てる
2年生の乗法九九の交換法則について、学習指導要領解説【算数編】には次のような記述があります。
- 乗法の計算の結果を求める場合には、交換法則を必要に応じて活用し、被乗数と乗数を逆にして計算してもよい。(p115)
- 乗法についての交換法則について 児童が自ら調べるように指導する。(p116)
- 乗法九九を構成するときに(中略)、乗法についての交換法則などを活用し、効率よく乗法九九などを構成したり、計算の確かめをしたりすることも大切である。(p116)
このことから、教師は交換法則を教えるという立場ではなく、児童自ら交換法則に気付き、それを生かそうとする姿を育てる立場であると解釈できます。

このような学習ができるいい教材はないか探していたところ、「算数教育の論争に学ぶ」(手島勝朗著・1988年発行・明治図書出版・絶版)という本のp35で、「口遊(くちずさみ)」(源為憲著・970年)の乗法九九を知りました。これは、当時の貴族の子弟のための教科書で、書物で見られる日本最古の乗法九九だそうです。国立国会図書館デジタルコレクションからも閲覧できます。
この乗法九九には、以下の特徴があります。
- 「九九八十一」から始まり、「八九七十二」「七九六十三」のような掲載順(乗数を固定して被乗数を1ずつ減らしていく)になっていること。
- 現在使われている総九九(81通り)ではなく、半九九(交換法則を適用した45通りの九九)であること。
- 二十は「廿」、三十は「丗」、四十は「卌」の漢字を用いていること。
- 「四八丗三」「一〃二」の間違いや「五八四十」「一二六」に削除線やあること。
- 「一五(五)」の虫食いなどがあること。
口遊の九九
この乗法九九を子供たちに提示すると、読めない漢字である3.で違和感をもちますが、もっている知識から推測して理解できると考えられます。また、2.のように少ないことに疑問をもてば、交換法則に関わる「はてな?」につながります。4.のような間違いも、今ちょうど乗法九九を習っている子供たちには共感をもって見てほしいものです。5.は子供にとっては面白い話題になるでしょう。
理解が難しいのは1.です。中国で発見されている昔の乗法九九(敦煌漢簡や里耶木簡)も同じ掲載順であることから中国から伝わったと教えることはできますが、その理由は諸説あります。そのため、もし出ても深く扱わないことがよさそうです。
このような教材研究をして、授業に臨みました。
ちなみに、「算数教育の論争に学ぶ」に書かれている論争とは、次の9つです。(目次から抜粋、…以下は筆者が加筆)
- 四則併進説と四則単進説
…加減乗除を並列で扱うか、学年ごとに区切るかの議論 - 一大論争「順九九か総九九か」1
…順九九に落ち着く。「順九九」とは、被被乗数が乗数より小さいか、または被被乗数と乗数が等しい場合の乗法九九のこと。 - 一大論争「順九九か総九九か」2
…現在と同じ総九九に落ち着く。 - 九九の唱え方と指導順序
…乗数先唱と被乗数先唱と、各段の指導順序の議論 - 水道方式との「対話と論争」
…小数のかけ算における乗法の意味指導の議論 - わり算の意味と筆算形式
…包含除と等分除の指導順序や筆算形式の議論 - 大きな数の話
…3桁で区切るか4桁で区切るかの議論 - 「メートル法」制定への道
…尺貫法からメートル法へ - 現代化批判の項
…算数教育の現代化に対する批判と昭和52年版学習指導要領
著者の手島勝朗先生は筑波大学附属小学校で算数を教えていた方で(後に、上越教育大学助教授、聖徳大学教授)、研修会で何度かお話を聞いたことがありますが、主張も論拠も明快でこんな話し方をしたいと思いました。当然この本もまだ算数教育の研究を始めて間もない私でも大変分かりやすく読めました。
特に参考になったのは「5. 水道方式との『対話と論争』」です。「水道方式」とは、遠山啓氏が提唱した「一般から特殊へ」の原則に基づいた指導のことで、タイル図を用いた計算指導や1あたり量を使った乗法の意味付けなどがあります。子供が算数を分かるようにしたいという願いのもと、どのようなアプローチをしていたかが垣間見ることができました。
この本は絶版ですが、CiNii(全国の大学図書館等が所蔵する本の情報を検索するサイト)で検索すると、約40件ほどヒットします。興味のある方は、近くの大学図書館で探してみてください。
授業の様子
はてな?
まず、今から約千年前の教科書に乗法九九が掲載されていたことを伝えました。
「千年!!」
「千年前にも九九を習っていたんだ…。」
「見てみたい!」
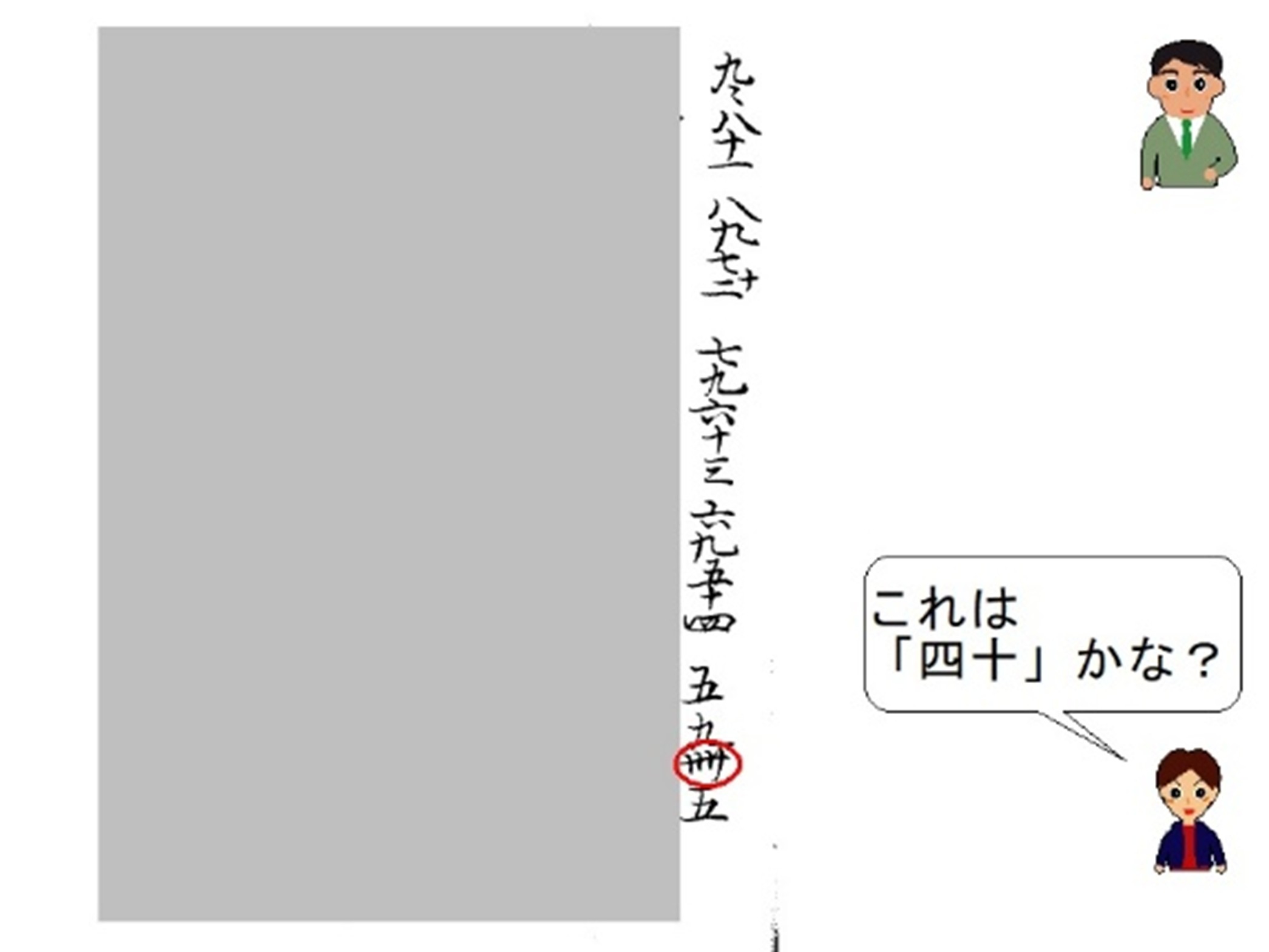
と興味津々です。さっそく電子黒板に口遊の九九の一行目だけを映しました。
「え?漢字なの!」
「あれ?(『卌』」を空書きしながら)なんて読むのかな?」
「『四十』かな?だって、『5×9=45』だから。」
「なるほど…」
特に挙手させなくても、既習の九九から「卌」は「四十」であることが子供たちだけで類推できました。この後に出でくる「廿」「丗」も、「二十」「三十」であることも同じように類推できました。
今、口遊の乗法九九を一行ずつ提示しましたが、もし、これを一度にすべて提示したら、どんな展開になっていたことでしょう。
たぶん、話題がいろんなところに飛び、みんなで力を合わせて考えれば解ける問題も解けなくなってしまいます。また、教師もその情報を整理することに力が割かれてしまいます。そこで、あえて一行ずつ隠して提示することで、自然に話題が焦点化されるようにしました。結果、子供の力だけで解決できる場面を生むことができました。

「あれ?間違いを見つけました!」
とAさんが大きな声で言ったので、説明をさせました。
「『4×8=32』なのに『33』になっています。」
この説明を聞いて、周りの子たちも頷き始めました。
「みんなは4の段は得意かな?先生は子供のころ苦手で、何度練習しても『4×7=16』になって困っていました。だから、これを書いた人の気持ちが分かるなあ…。」と語ってみました。
すると、
「そうそう、私も分かる!」
「私も分かる、7の段が苦手だもん…。」
「自分も間違わないように気を付けよう!」
と数人から間違いに対する共感するつぶやきが聞こえてきました。
乗法九九の習いたてのころは、意味理解が浅いまま音で覚えるため、時間は経つと発音の似ている箇所の記憶が曖昧になっていきます。それを修正するには、そこを間違った箇所を意識させることと、何度も正しい乗法九九を唱えることが必要です。
経験上、間違いを指摘し合う学級の雰囲気ではなかなか乗法九九の暗唱がうまくいかなかったと感じていました。いろいろな場面で「間違っても大丈夫!次は気を付けよう」という学級の雰囲気を作ることが、乗法九九の暗唱の習得だけでなく、ほかの学習でもいい効果を生むと思います。

口遊の乗法九九をすべて提示しました。これを見たときに、できれば、多くの子が「九九が少ないなあ」と思う場面を作りたいです。
そこで、「全員、起立!」と全員立たせました。そして、この乗法九九を見て、何か気付いたことはないか考えさせ、思いついた人から座るように指示しました。(この手法の詳細は第2回や第7回、第9回を参照ください。)
あっと言う間に全員が座りました。
一言ずつ、全員に気付いたことを言ってもらいました。
「少ない。」
「足りない。」
「順番が違う。」
「1の段が少ない」
…などの声を聞くことができました。
「『少ない』や『足りない』」が多かったですね。九九表で確かめると、何か分かるかもしれないよ。」と発問し、口遊の乗法九九と九九表が並んだワークシートを渡しました。
なるほど!
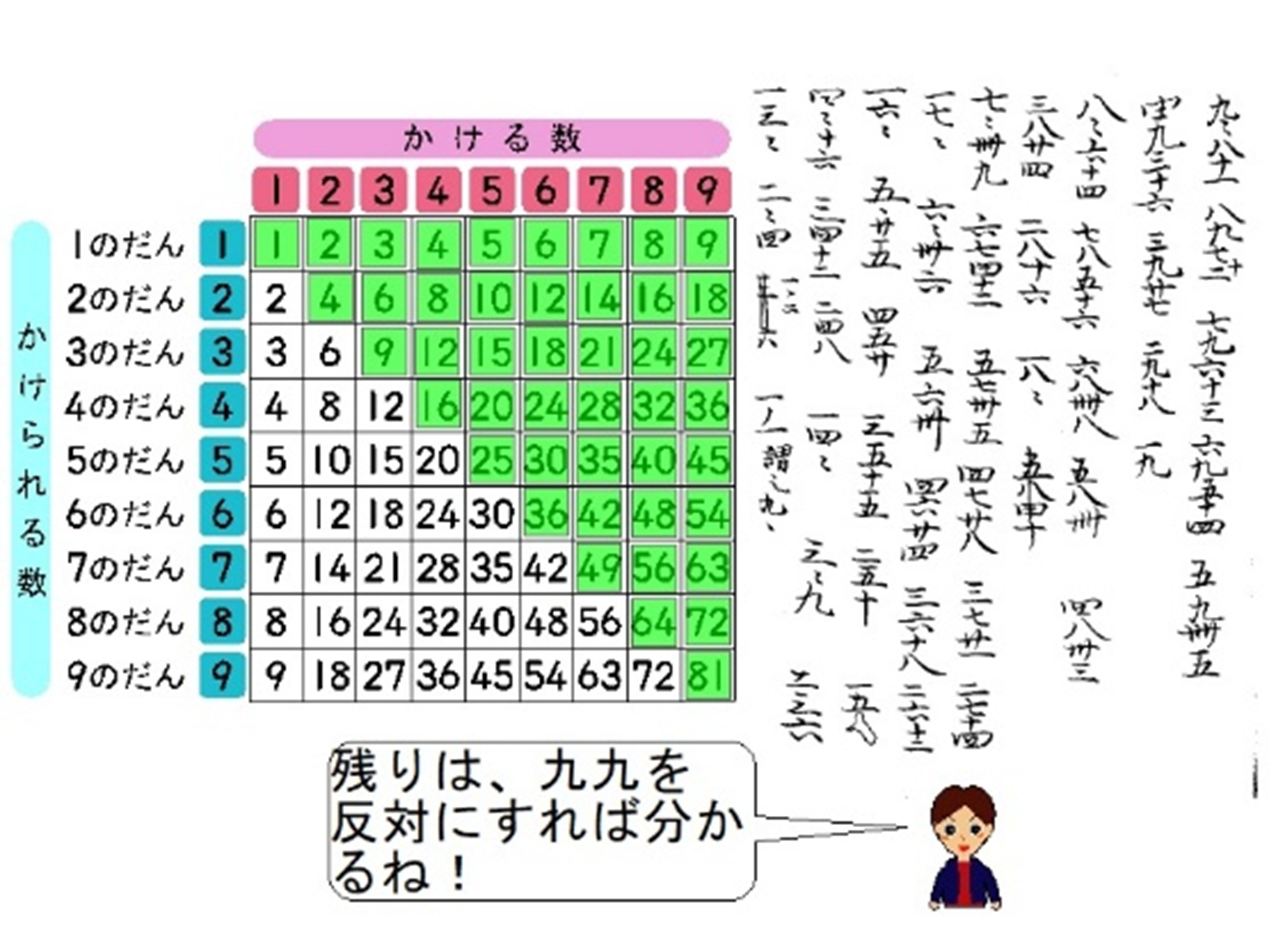
みんなで一緒に、口遊の乗法九九を読み上げながら、九九表のその箇所を塗りつぶしていきました。
「『九九八十一』は『9×9=81』」
「『八九七十二』は『8×9=72』」
「『一ノ一』は『1×1=1』」
最後の口遊の乗法九九を読み上げたときです。
「分かりました!」
とBさんが手を挙げました。Bさんにそのまま説明させたいところですが、CさんやDさんも少し遅れて手を挙げました。
そこで、Bさんが何を言いたいか、CさんとDさんに予想してもらい、最後のBさんで確かめることにしました。
Cさん「たぶん、私の考えと同じで『塗ってない部分は九九を反対にすると分かる』と思います。」
Dさん「私も同じで『九九を反対にすると分かるから少なくていい』だと思います。」
Dさんが「同じです。」で終わりそうな場面ですが、全く同じということはほとんどありません。また、発表する力を高める機会ですから、これを生かさないともったいないです。
そこで、このように同じような内容を発表させるような場面では、前の人と違った部分を褒めています。上のDさんであれば、「少なくて」を付け足した点を大いに褒めてあげました。
最後に、Bさんに発表させました。
「九九を反対にすると少なく覚えてすむから、昔の人は頭がいいと思いました。」
「『昔の人は頭がいい』と考えたのがいすごいなあ!」と褒めてあげると、自然に拍手が起きました。
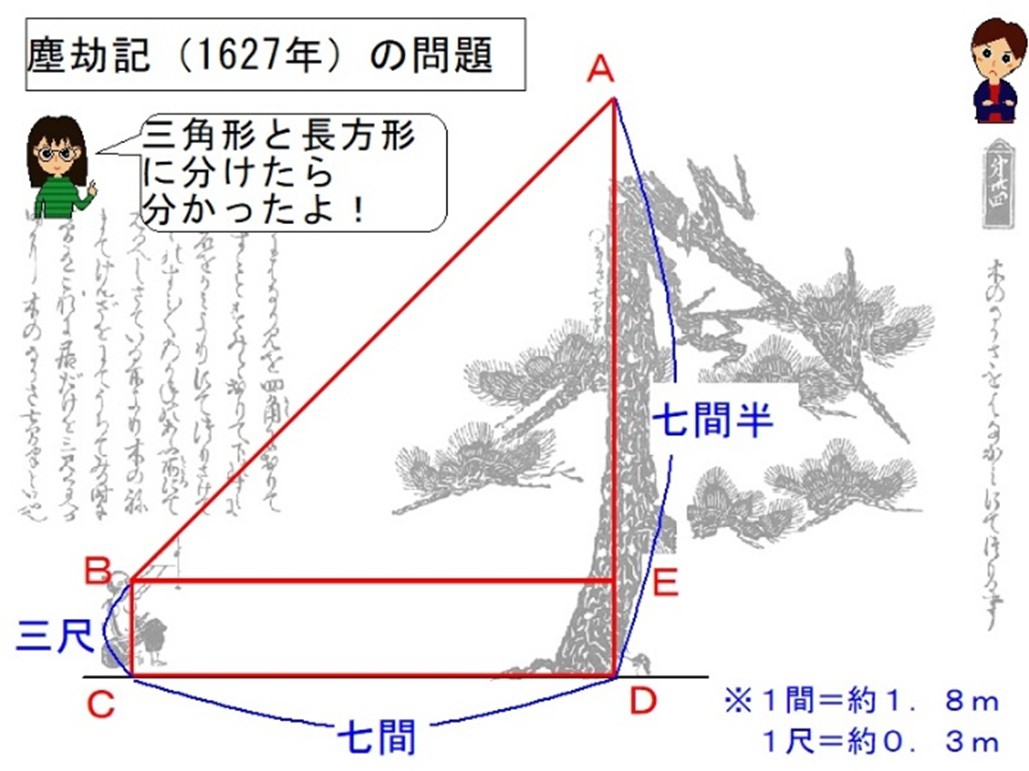
「次回は、6年「比とその利用(塵劫記)」を取り上げます。お楽しみに!
※今回は「だったら…」はありません。

種市 芳丈(たねいち よしたけ)
小中一貫三戸学園 三戸町⽴三戸⼩学校・三戸中学校 教頭
子供たちが夢中になる算数授業づくりに取り組んでいます。算数専科や複式学級の指導の経験あります。今、チャレンジしているのは、ロイロノートを活用した算数授業です。算数の教材づくりの会「ガウスの会(代表:細水保宏)」の会員。
関連記事
- 昔の算数に挑戦2<6年「比と比の値(塵劫記)」>
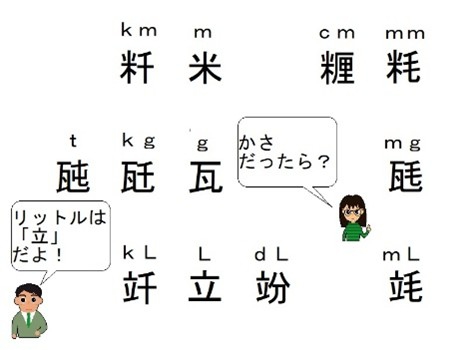
- 子供の「だったら...」を引き出す教材3<6年「単位の仕組み」>
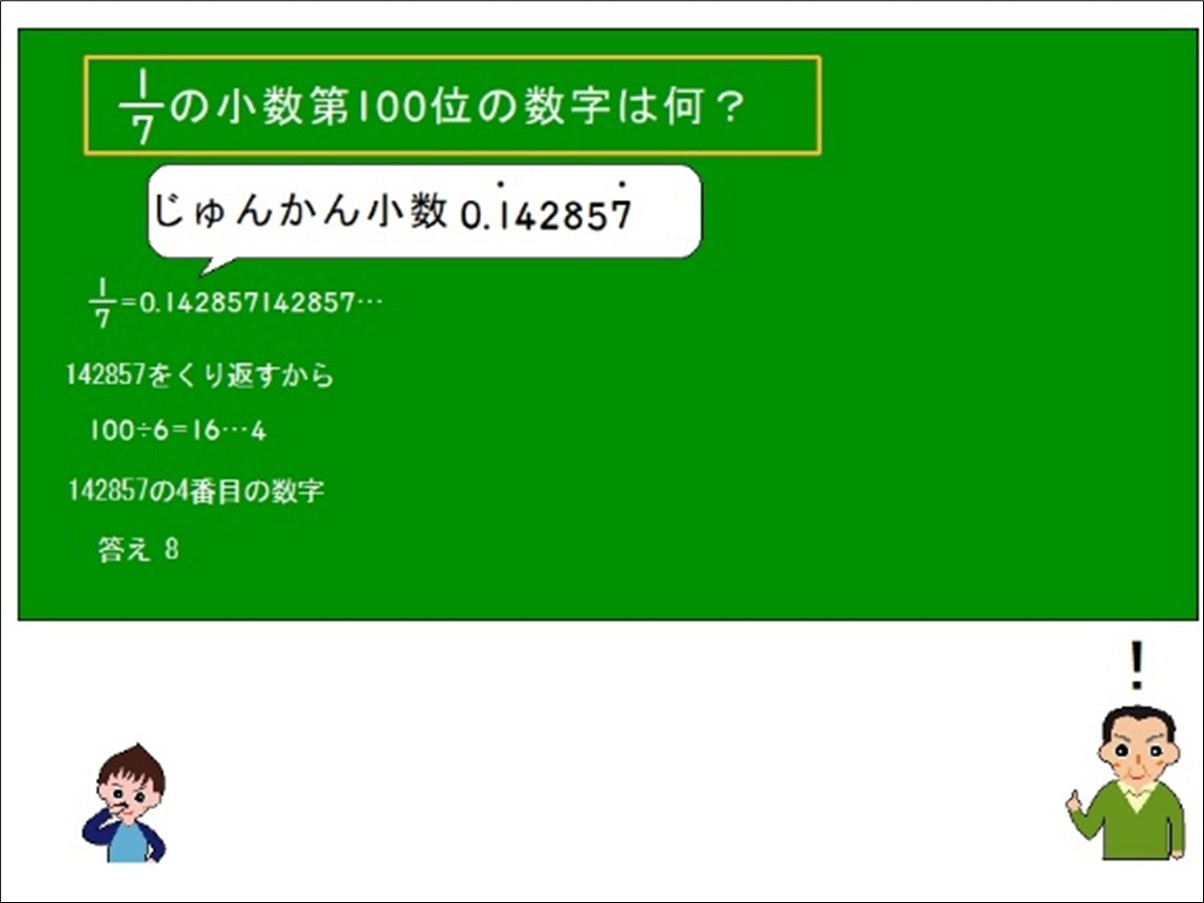
- 子供の「だったら...」を引き出す教材2<5年「小数と分数(循環小数)」>
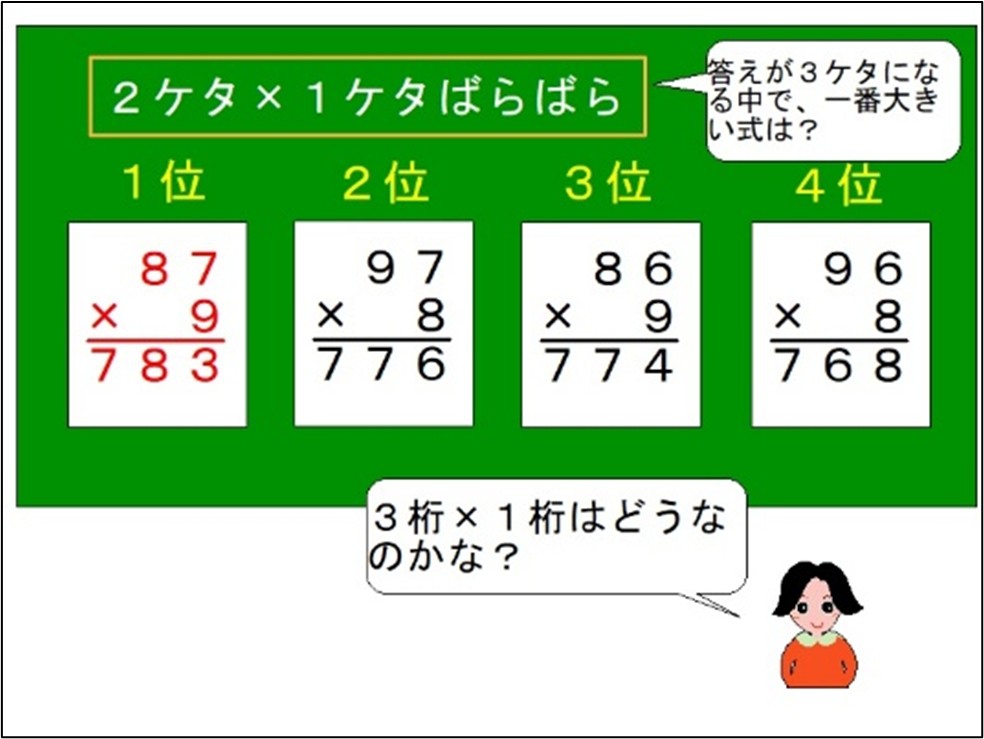
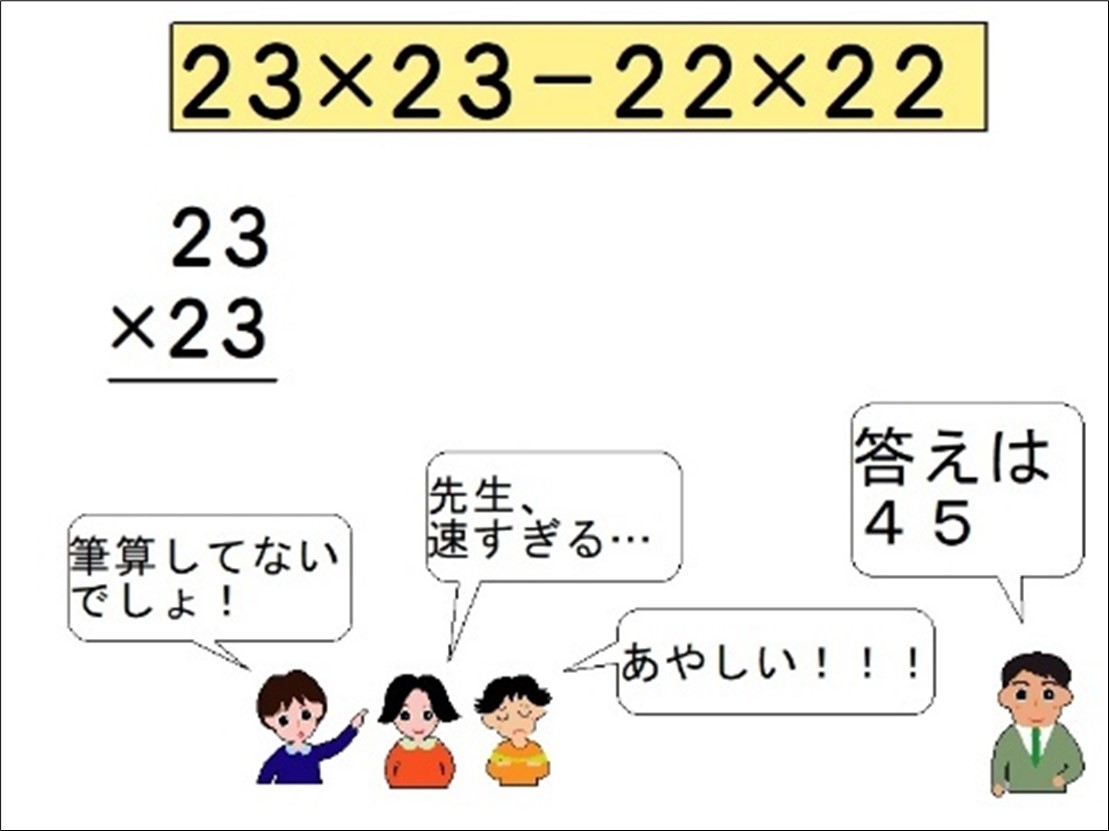
- 子供の「だったら...」を引き出す教材<3年:かけ算の筆算>
- 既習を生かして「なるほど!」を作り出す3<5年:小数のかけ算>
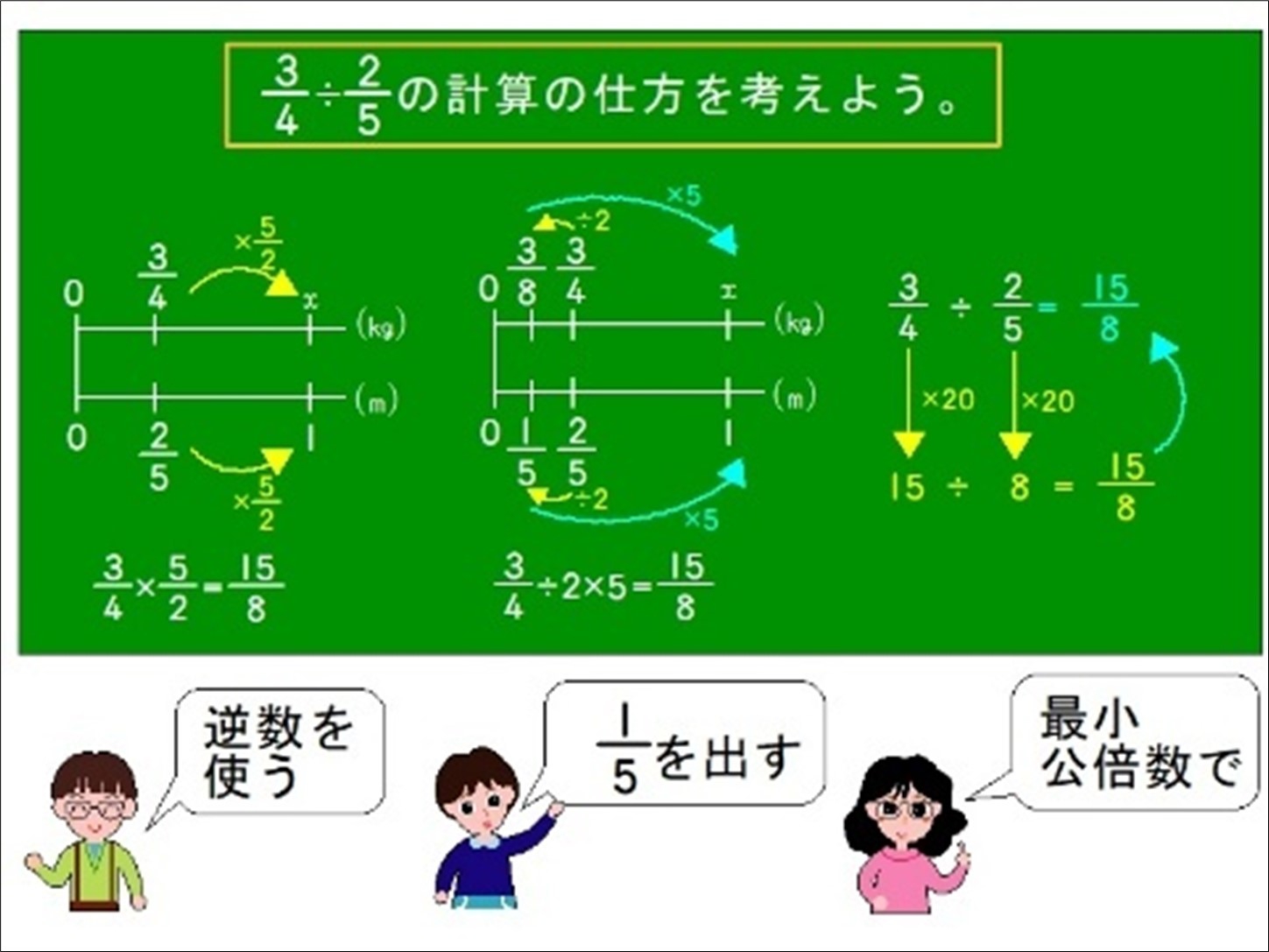
- 既習を生かして「なるほど!」を作り出す2<6年:分数のわり算>
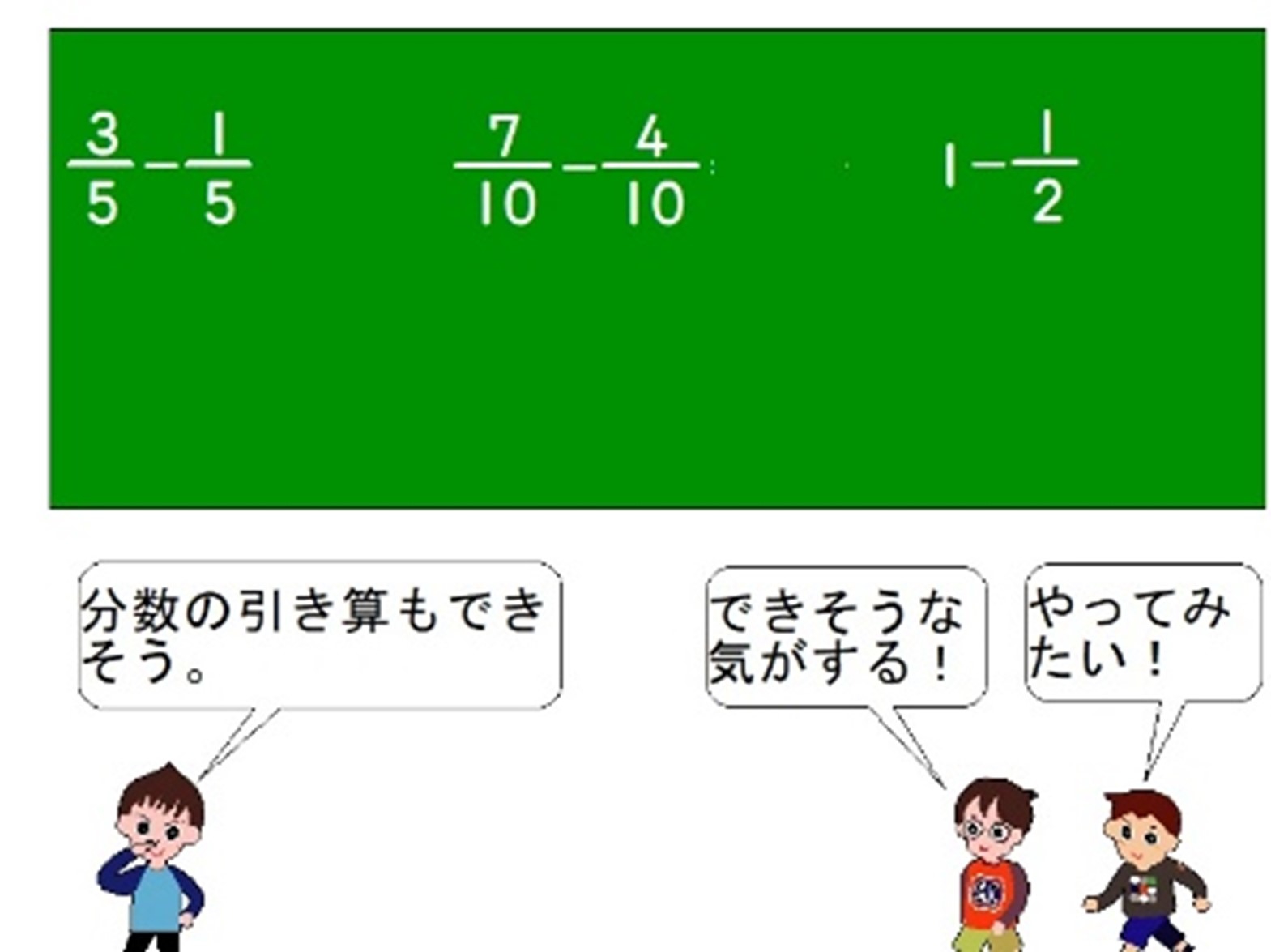
- 既習を生かして「なるほど!」を作り出す<3年:分数のひき算>
- 算数手品で「はてな?」を引き出す2<3年:かけ算の筆算>
- 算数くじで「はてな?」を引き出す<3年:かけ算>
- 算数手品で「はてな?」を引き出す<3年:たし算の筆算>
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生




 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事