子供の「だったら...」を引き出す教材２＜５年「小数と分数（循環小数）」＞ 「はてな？」「なるほど！」「だったら…」で作る算数授業（第8回）

分数を小数にする時に、ある桁から同じ数字の列が無限に繰り返される小数になることがあります。 これが循環小数です。例えば、「13＝０．３３３３…」や「17＝０．１４２８５７１４２８５７…」などがあります。

学習指導要領では高校の数学Ⅰで扱われることになっていますが、中学校３年の「有理数と無理数」でトピックとして紹介されることもあります。

また、計算技能面だけで考えると、小学校４年で習う「わり進むわり算」ができれば求められます。また、小学校５年の「分数と小数」で子供の考えを生かして授業していると、13や111などの循環小数になる分数が自然に出でくるので、５年の「分数と小数」の発展として扱うこともできます。

しかし、小学校の教科書やワークなどで見かけることがなく、算数教育の書籍でも先行事例を見かけることがなかったため、しばらく教材化を躊躇していました…。

そんな中、当時勤めていた学校の図書館で「算数と理科の本〔17〕ふしぎな小数」（銀林浩著・1980年発行・岩波書店・絶版）という本を見つけました。解説を読むと、このシリーズは、小学校４～６年生で習う算数と理科の中から、子供たちが興味をもち、学習のもとになるテーマを選んで作られたそうです。

読み進めていくと、教材化のヒントとなる以下のようなことが書かれていました。

• 循環小数の表し方
繰り返す部分の数字の始まりと終わりに「・」を付ける。
例：17＝０．１４２８５７１４２８５７…＝０$\stackrel{・}{\mathrm{１}}$４２８５$\stackrel{・}{\mathrm{７}}$

• 循環小数の循環節と周期
例：1 7 の循環節は１４２８５７、周期は６

• ダイヤル数字（１４２８５７）の性質
例１：１４２８５７×２＝２８５７１４
例２：１４２８５７×７＝９９９９９９

• 循環小数を分数にする方法
例：ｘ＝０．$\stackrel{・}{\mathrm{５}}$　　…（ア）
　　両辺に１０をかけると
　　ｘ×１０＝５．$\stackrel{・}{\mathrm{５}}$　　…（イ）
　　（イ）－（ア）をすると
　　９×ｘ＝５
　　ｘ＝5 9

今回紹介する「小数と分数（循環小数）」は、前述の本を参考にして、子供たちに循環小数を作らせます。実践にあたり、次の３つの工夫をしています。

①循環小数を使った問題に変更する
無限小数になる分数は、教科書では「17を四捨五入して1100の位までの小数で表しましょう」という扱いでした。
そこで、問題を変更し、「17の小数第１００位の数字は何？」に変更します。（最近の教科書では、小数の位の名称は110の位、1100の位…、のみですが、この実践の取り組んだ時は、小数第１位、小数第２位…、の両方が掲載されていました。）

②□を使って問題と関わりやすくする
はじめから「小数第１００位」と提示すると、どうやって取り組めばいいか分からず止まってしまう子がいることが予想されます。
そこで、１００の部分を□で隠して「17の小数第□位の数字は何？」とはじめに提示します。
これにより、子供たちは自分がまず取り組める数値である「１」や「２」を入れて考え始めることでしょう。

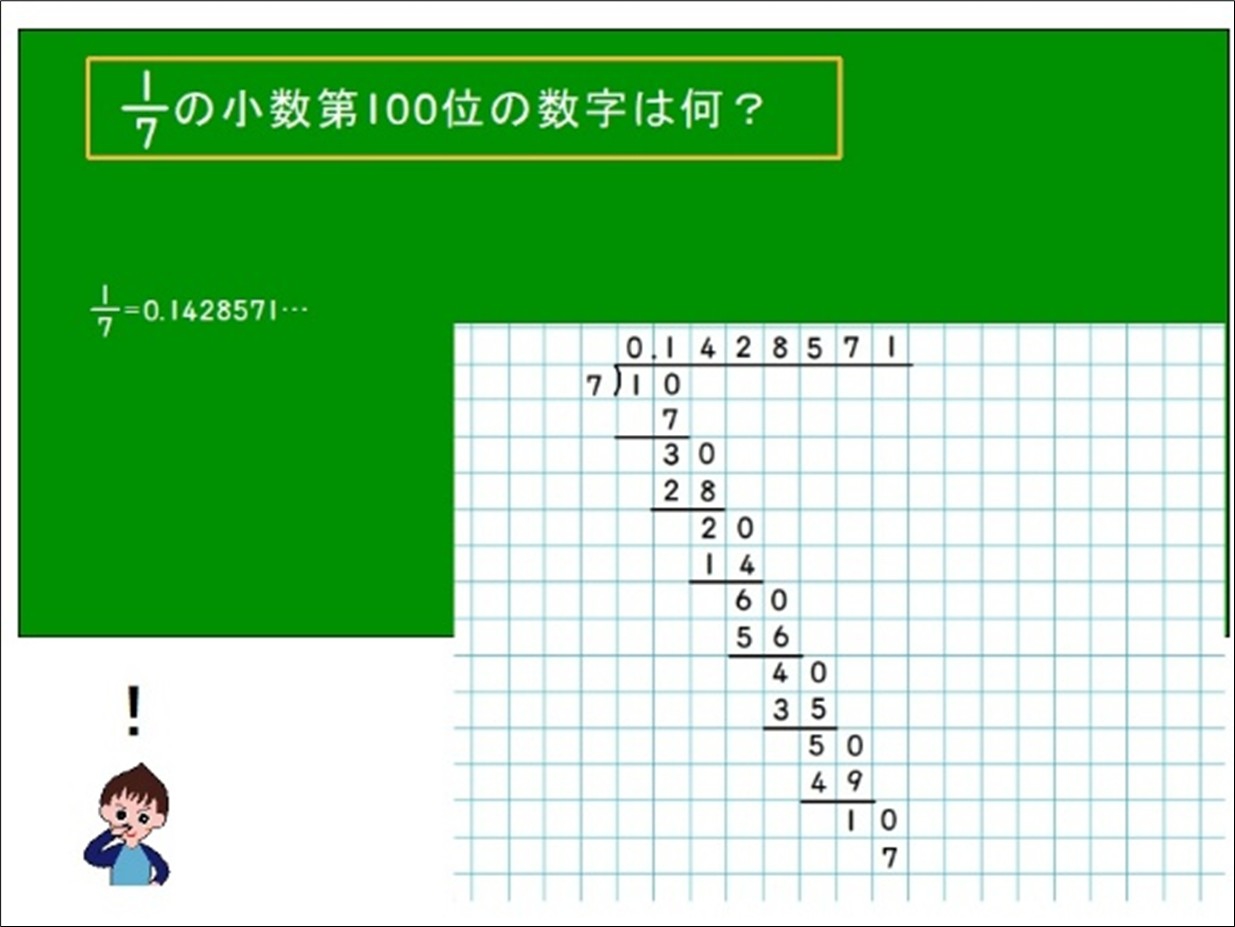
それを「１÷７」の筆算で確かめながら、割り進めていきます。「０.１４２８５７１」まで割り進めた時点で、隠していた□を外し、１００を提示します。

③計算力に応じて個に応じた指導を行う
循環小数になる分数を探す場面では、計算が得意な子たちは水を得た魚のようにどんどん動き出しますが、計算の苦手な子は動きが重くなります。
そこで、計算間違いしたり計算が苦手だったりする子たちには、友達と相談したり電卓を使ったり教師に計算を見てもらったりしてもいいことを促します。このような個に応じた指導を行うことで、自分で考えたついたことが形になったという成就感を味わえるようにします。

まず、黒板に「17の小数第□位の数字は何？」と書いてある紙を貼りました。

「□の下の数字を隠れているね。」
「□の下が１だったら、簡単！」
とつぶやきが上がりました。

「□が１だったら簡単と聞こえたけど、どうやって求めるのかな？」と問い直すと、Ａさんが説明してくれました。
「『１÷７』を計算すると出せます。さっき計算したら小数第１位の数字は１でした。」

その説明に合わせて、実物投影機で映したマス目のある算数ノートに筆算を書き込みました。

わり算の筆算の間違いの原因のひとつに位を揃えないで計算することが挙げられます。そのため割り進めるうちに筆算が曲がっていったり、字の大きさがまちまちなため位がずれたりする子をたくさん見かけてきました。

それを防ぐためには、実物投影機で映してマス目に計算することを促しました。

□を７まで進め、「17＝０．１４２８５７１…」まで計算しました。

教室のところどころで、
「あれ？見たことがあるぞ…」
「『１』がまた出てきた！」
「繰り返しパターン？」
など数人が同じ計算を繰り返すことに気付き始めてきました。

今が今日の問題を知らせる頃合いと判断し、すかさず□を外し、「１００」を提示しました。

「え？１００！！！」
「それはちょっと無理…」
とあきらめ気味の子がいる中で、Ｂさんがすっと手を挙げました。

「まだ計算してないんだけど…、たぶんこのあとも１４２８５７を繰り返すでしょ。つまり、１００の中に６のかたまりが何回取れるか計算して、あまりを出す。そのあまりの数で何の数字が出るか分かるはず。」

教室が一瞬シーンとなりました。あまりに整然とした説明に、聞いているみんなが追いついてきていないようです。そこで、Ｂさんの説明を区切りながら、黒板に式で書いていくことにしました。

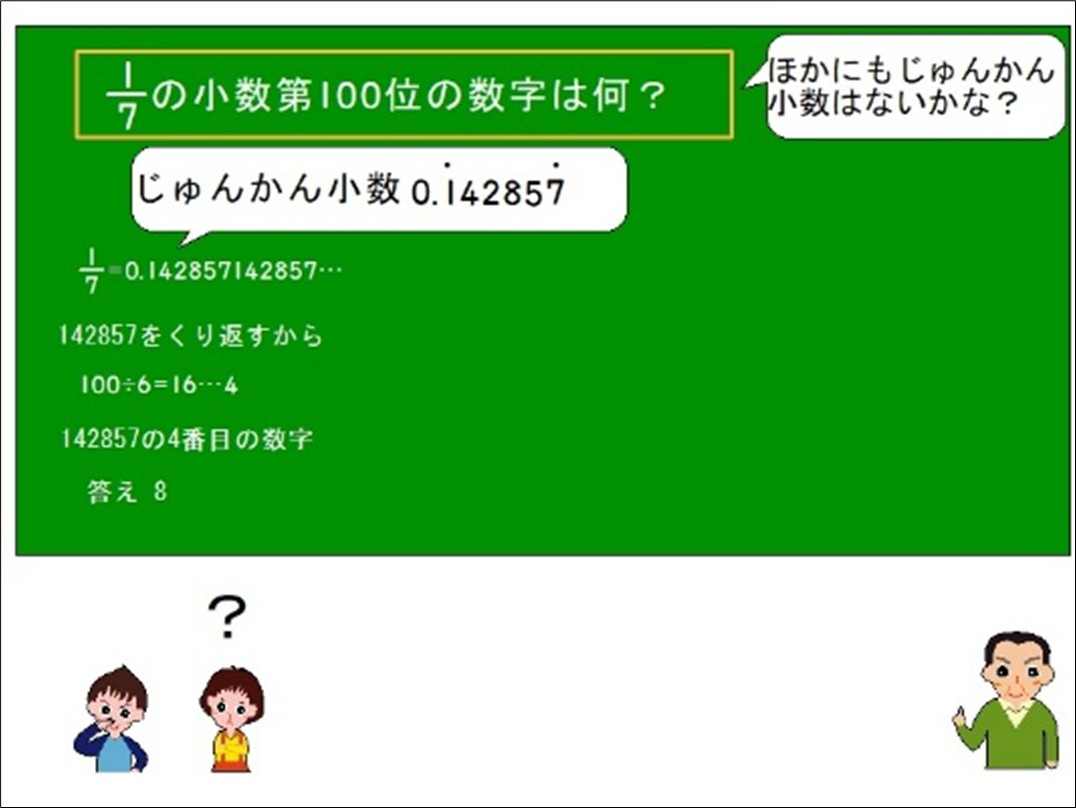
Ｂさんの考えを式に表すと以下のようになりました。

17＝０．１４２８５７１４２８５７…
１４２８５７を繰り返すから
１００÷６＝１６…４
つまり、１４２８５７の４番目の数字
答え　８

周りから自然に拍手と称賛のつぶやきが起きました。
「すごいね！」
「天才！ねえ、どうしてこの解き方を思いついたの？」

発想の根源を問う質問が自然に出ました。私も「先生も知りたいな、きっとほかの子の参考になると思うから教えてくれるかな？」とその質問に乗っかりました。

すると、Ｂさんはこう答えました。
「前にカレンダーの曜日を考える問題があって、『１日が月曜日だと、２０日は何曜日？』みたいな。このときは７で割って、そのあまりから月曜日から順番に曜日を数えたから、この問題も似ていると思った…」

これを聞いて、「なるほど～！」とみんなうなずきました。

子供たちに、このように繰り返す小数のことを循環小数と呼ぶことと表記の仕方を教えました。

じゅんかん小数　０$\stackrel{・}{\mathrm{１}}$４２８５$\stackrel{・}{\mathrm{７}}$

「『じゅんかん』って社会科で出たような…」
「『１』って点を付けるアイディア、便利だな。」
とつぶやきが聞こえる中で、Ｃさんから次のような問いが出ました。

「ほかにも循環小数（になる分数）はないのかな？」

みんなに同じように考えた子はいないか尋ねてみると、半分くらいの子が手を挙げました。

「いい『はてな？』です。今日はこれをみんなで考えましょう。」と言いながら黒板にＣさんの問いを書きました。このように、子供から出た問いを褒めたり取り上げたりすることは、問い方を教えることにつながります。また、同じような問題に出合った時、自ら「はてな？」と動き出すことでしょう。

まず、自分で循環小数になる分数を探す時間を７分間とりました。机間巡視をすると、以下のような様子でした。

ア：1 2 や1 3 などの単位分数の分母の数字を順番に大きくして計算している子

イ：2 7 や3 7 など分母が７の分数の分子を順番に大きくしている子

ウ：鉛筆を持って止まっている子

アやイの子は、そのまま自分だけで考える時間をとってあげるのがよいですが、ウの子はこのまま何もしないで時間が過ぎるかもしれません。そこで、まずウの子たちには電卓を渡して思った分数を計算してみるように声をかけました。

ウの子たちは、「１÷２」「１÷３」などを計算し始めました。

７分経ちました。自分で見つけた循環小数になる分数を発表してもらいました。

「2 7 ＝０.$\stackrel{・}{\mathrm{２}}$８５７１$\stackrel{・}{\mathrm{４}}$」
「3 7 ＝０.$\stackrel{・}{\mathrm{４}}$２８５７$\stackrel{・}{\mathrm{１}}$」
「1 3 ＝０.$\stackrel{・}{\mathrm{３}}$」
「2 3 ＝０.$\stackrel{・}{\mathrm{６}}$」
「1 11 ＝０.$\stackrel{・}{\mathrm{０}}\stackrel{・}{\mathrm{９}}$」
もっとたくさん見つけていたのですが、循環小数を分数にする方法の時間をとるため、ここで切りあげました。

子供たちに、何か気付いたことはないか尋ねてみると、
「分母が７の分数は、出でくる６つの数字は同じだけど、先頭になる数字が違う。」
「4 7 や5 7 もあやしい。」
「2 11 や3 11 もあやしい。」
など、とてもいい気付きがありました。

普段は子供の「だったら…」を取り上げますが、今回は教師からの「だったら…」です。自分が感じた楽しさを伝えるためです。

「実は、自分で適当に作った循環小数を分数にする方法があります。少し難しいけど知りたいかな？」と投げかけてみると、

「知りたい、知りたい！」とかなりの子が前のめりになりました。

きっと、循環小数のもつ不思議さを感じた子が多かったのでしょう。数学者のフリードリヒ・ガウスも循環小数の不思議さに魅了されたひとりで、周期がどのように決まるかを調べていたそうです。

循環小数を分数にする方法を０.５で説明しました。
ｘ＝０．$\stackrel{・}{\mathrm{５}}$ 　…（ア）
両辺に１０をかけると
ｘ×１０＝５．$\stackrel{・}{\mathrm{５}}$　 …（イ）
（イ）－（ア）をすると
９×ｘ＝５
ｘ＝5 9

説明を聞き終わると、
「『０．$\stackrel{・}{\mathrm{１}}$』はどんな分数かな？」
「『０．$\stackrel{・}{\mathrm{１}}$２$\stackrel{・}{\mathrm{３}}$』でやってみる！」
と意欲的に取り組み始めました。

難しいと思った子たちには、「友達と一緒にやったり、電卓を使ったりしてももいいよ。」と声をかけ、取り組ませました…。

※０．$\stackrel{・}{\mathrm{１}}$＝1 9 、（両辺に１０００かけて）０．$\stackrel{・}{\mathrm{１}}$２$\stackrel{・}{\mathrm{３}}$＝123 999 ＝41 333

次回は、６年「単位の仕組み」を取り上げます。お楽しみに！