算数の教え上手
学校の危機管理
世界の教育事情
今どきの小学生
【天文シリーズ】星の距離はどうやって測るの？
前回、私たちの住んでいる地球は、太陽という自ら輝く恒星のまわりを周る、小さな惑星であり、水星、金星、火星、木星、土星などの惑星とともに太陽系を形成している事、また、その太陽系は天の川銀河と呼ばれる、大きさが10万光年という非常に大きな円盤型をした何千億個もの星の集団に属していることを説明しました。
ところで、私たちがそのような宇宙の描像を得るためには、星までの距離を知る必要があります。それでは、星の距離はどのようにして測定するかご存知でしょうか。
実際には距離の測定方法は色々あるのですが、代表的で最も基本となっている方法のひとつとして、三角測量と呼ばれる方法があります。
この方法は測定したい対象（ここでは星）を、異なる２つの場所から見ることでその星の見える方角が微妙にずれますが、そのわずかな角度のずれから距離を測定する方法です。もう少し具体的にいいますと、地球は太陽の周りを1年かけて1周まわりますが、異なる時期（例えば春と秋、もしくは夏と冬）に地球が異なる場所にいることを利用します。地球の軌道上の異なる2ヶ所から星を観測して、その異なる場所から見る星の方向のわずかなずれを測定すれば星までの距離が分かります。
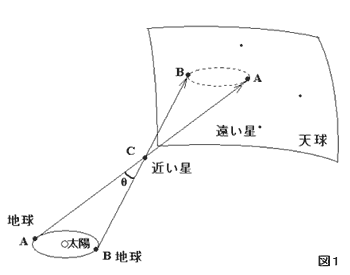
図１を見てください。地球が太陽のまわりを周っていますが、Aにいる時とBにいる時で「近い星」の見える方角が微妙に違います。その角度のずれは図でいえば、三角形ABCの角C、すなわちθに相当する角度です。この角度θを測定することで、太陽と近い星との距離を見積もる事が出来ます。
この三角測量は星までの距離をはかるためだけに用いる特別な方法ではありません。私たちの日常でもありふれた馴染み深いものです。
実際、私たちもこの三角測量を利用して距離を見積もっている事はご存知でしょうか。異なる2箇所から対象を見るのが三角測量のポイントでした。私たちは2つの眼を利用して対象を見ています。2つの眼から見た、対象の方向のわずかなずれを利用して距離を見積もっているのです。
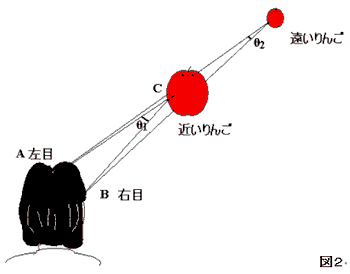
例えば、近いりんごの場合、左目のAと右目のBという異なる場所から見る事で、りんごの見える方角が角度θ1だけずれます。遠いりんごの場合θ2だけずれます。これを認識して私たちはりんごまでの距離を見積もります。しかも人間は驚くことに、2つの眼で見たわずかなずれを考察したり、計測したりなどはしておらず、瞬間的に理解し距離をつかんでいます。見積もっているという認識は全くありません。対象までの距離が自然に理解され、立体的に世の中を見ることが出来ています。
ところで、私たちが距離を見積もる時、どの程度の角度を見分けているでしょうか。また星の距離を測定する時、どの程度の角度のずれを測定しなければならないのでしょうか。
例えば、人間が5m先のりんごの距離を見積もるのにどれくらいの角度のずれを認識しているかといいますと0.7°程度です。人間はもっと遠くの距離を見分けられる事を考えますと0.7度よりは小さい精度で見積もることが出来ています。最も近い恒星（ケンタウルス座α星）を眼で見極めるためには0.0000000000000001°という非常に小さい角度のずれを識別できなければなりません。もちろんこれは不可能であり、星の距離を眼で識別はできません。
執筆：矢野太平
※当記事のすべてのコンテンツ（文・画像等）の無断使用を禁じます。
この記事をクリップ
クリップした記事この記事に関連するおススメ記事
「おすすめ特集記事」の最新記事
