一筆書き
鉛筆などの筆記用具のペン先を紙からはなさないで,一度書いた線の上を通らないようにして,線で図を書くことを「一筆がき」といいます(ただし,同じ点は何度通ってもよい)。図形を一筆がきでなぞるとき,一筆書きができるものと,どんなに工夫してもできないものがあります。何か違いがあるのでしょうか?うまく見分ける方法はあるのでしょうか?
準備体操
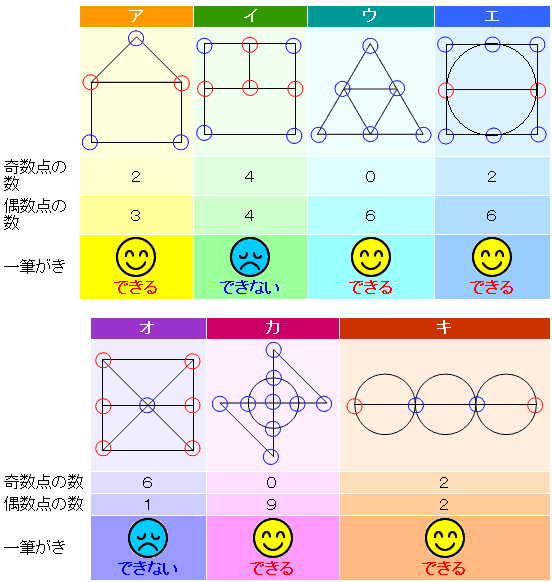
次の図は一筆がきができますか。

解説
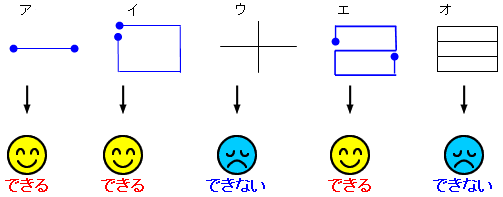
ア、イ、エは一筆がきができますが、ウとオはどんなに工夫しても一筆がきはできません。
一筆がきができる図とできない図の違いはなんでしょうか?
その秘密は、図の頂点(とがっている部分)や線の交点や線の先端の点に注目するとわかります。そして、一つの点(頂点や交点)から出ている線の数が奇数か偶数かを確認します。奇数個の線が出ている点を奇数点、偶数個の線が出ている点を偶数点とよぶことにします。
例えば、エの図だと次のようになります。
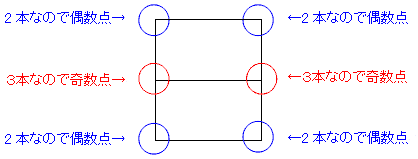
そして、奇数点と偶数点の数を数えます。この図だと、奇数点が2つ、偶数点が4つです。
他の図も確かめてみましょう。偶数点を○、奇数点を○として次の表にまとめてみました。
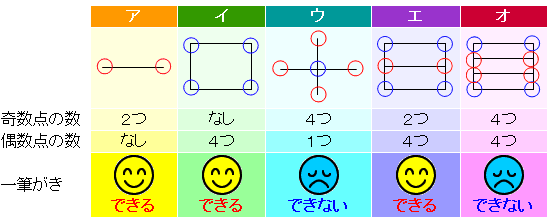
ここでは多くの例を出すことはできませんが、一筆がきができるかできないかは、奇数点の数と偶数点の数できまります。結論は次の通りです。上の表で確かめてください。
・偶数点だけでできている図(奇数点がない図)は一筆がきができる…イ
・奇数点が2つの図は一筆がきができる…アとエ
これ以外の条件では一筆がきができません。例えばオは奇数点が4つもあるので、一筆がきはできません。
さらに、一筆がきの問題では、どこから書きはじめてどこで終わるかということもポイントになります。
・偶数点だけでできている図(奇数点がない図)はどこから書きはじめても必ず出発点に戻る…イ
・奇数点が2つの図は一つの奇数点から書きはじめて、もう一方の奇数点で終わる。…アとエ
答え:ア、イ、エ
問題1
次の図で、一筆がきができるものはどれですか。
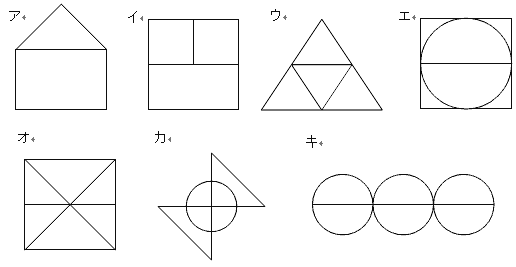
解説
準備体操で説明したように奇数点と偶数点も調べてみます。偶数点を○、奇数点を○で印をつけます。
正解はア、ウ、エ、カ、キです。実際に書いて確かめてみてください。
その際、偶数点だけの図は必ず書き始めた点に戻ること、奇数点が2つの場合は奇数点からはじまり、もう一方の奇数点で書き終えることも確認してください。
答え:ア、ウ、エ、カ、キ
問題2
次の図を一筆がきで書く方法は何通りありますか。ただし、スタート地点が違う場合は異なるものとして数えます。
解説
まず、奇数点と偶数点を確認してみます。奇数点と偶数点も調べてみます。偶数点を○、奇数点を○で印をつけてみます。
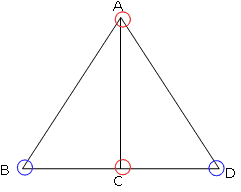
奇数点が2つなので、確かに一筆がきができることがわかります。
さらに奇数点が2つなので、一筆がきの書きはじめと書きおわりは、
AからはじまりCで終わる場合
CからはじまりAで終わる場合
の2つのパターンがあります。
まずは、Aから書きはじめる場合を考えます。Bに向かう場合とCに向かう場合とDに向かう場合があります。
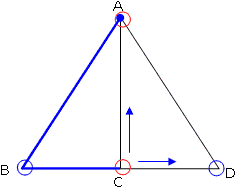
AからBに向かった場合は、必ずCに向かうことになります。
そのあとは、左まわりでCに戻る場合と右回りでCに戻る場合の2通りがあります。
つまり、
A→B→C→D→A→C
A→B→C→A→D→C
の2通りです。
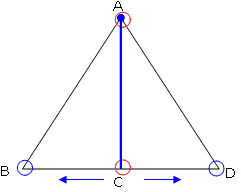
次にAからCに向かった場合は、
左まわりで(Dを通って)で三角形を1周する場合と右まわりで(Bを通って)三角形を1周する場合があります。 A→C→D→A→B→C
A→C→B→A→D→C
の2通りです。
同じようにして、AからDに向かった場合は、
A→D→C→A→B→C
A→D→C→B→A→C
の2通りです。
以上がAから書きはじめた場合で全部で6通りです。
次にCから書きはじめた場合はどうでしょうか?
同じように数えなければならないのでしょうか?
その必要はありません。なぜなら、この図は奇数点が2つあるので、Cからスタートした場合は必ずAに戻ります。つまり、Aから書きはじめた場合の逆順になります。ゆえに、これも6通りです。
Aから書きはじめた場合とCから書きはじめた場合を足して、正解は12通りです。

くり返しになりますが、奇数点が2つの場合の一筆がきは、必ず奇数点からはじまり、もう一方の奇数点で書き終えます。このことを覚えておかないとこの問題をスムーズに解くことができないでしょう。
答え:12通り
問題3
18世紀の初めごろにケーニヒスベルクという大きな町がありました。この町の真ん中には、ブレーゲル川という大きな川が流れており、七つの橋がかけられていました。あるとき町の人が言いました。
「このブレーゲル川にかかっている7つの橋を2度通らずに、すべてわたって、もとのところに帰ってくることができるか。ただし、どこから出発してもよい。」 町の人が言ったことはできるのでしょうか?
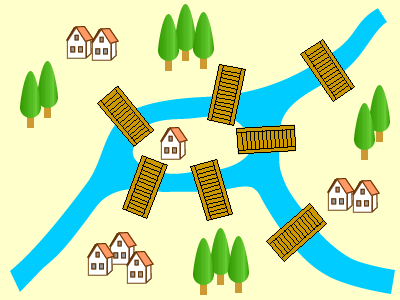
解説
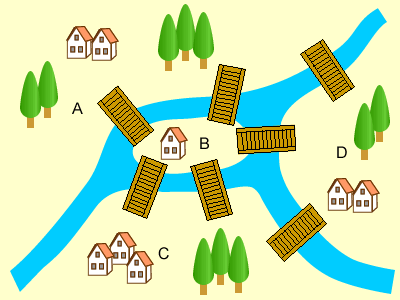
まず、次のように、それぞれの場所に名前(A、B、C、D)を付けます。
そして次のような図に置きかえます。
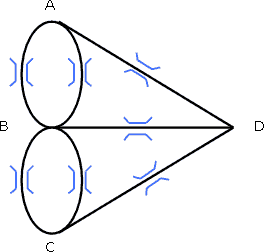
7つの橋を2度通らずに、すべてわたって、もとのところに帰ってくるということなので、この問題は一筆がきの問題に置き換えることができます。つまり、この図で一筆書きができるなら、「7つの橋を2度通らずに、すべてわたって、もとのところに帰ってくることができる」ということになります。
そこで、奇数点と偶数点を調べてみます。偶数点を○、奇数点を○で印をつけてみます。
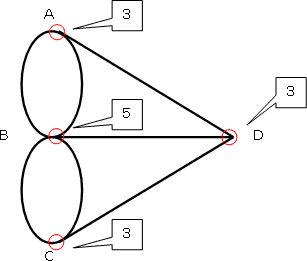
すると、4つともすべて奇数点です。一筆がきは、奇数点が0か2つ以外の図ではできませんので、この図では、一筆がきはできません。
ゆえに、「できない」が正解です。
この問題を町の人は真剣に考えましたが、誰も解けませんでした。解けない理由もわかりませんでした。結局、オイラーという数学者がここで説明したような一筆がきのきまりで解決しました。
答え:できない

教え上手 きんたろう先生
「算数の教え上手」担当のきんたろうです。よろしくお願いいたします。
私が塾・予備校で教壇に立つようになってから、10年近くになりました。どちらかというと、勉強があまり好きでない生徒を教えてきました。そんな生徒の中にも、きっかけを作ってあげると夢中になって勉強する子がいます。
そんなとき「いい仕事をした」と思います。
教え上手とは,もちろん科目を教えることが上手であることと思いますが、併せて子どもに学ぶ意欲を起こさせることだと思います。
この「教え上手」では、その両面について、私の経験を活かして述べさせていただく予定です。ご参考にしてください。
この記事に関連するおススメ記事

「おすすめ特集記事」の最新記事














 学校の危機管理
学校の危機管理 世界の教育事情
世界の教育事情 科学夜話
科学夜話 今どきの小学生
今どきの小学生



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事
