意外と知らない"算数・数学のつまずきポイント"(第2回) 算数・数学を生かせる仕事と、試行錯誤して学ぶことの大切さ

AIが数学者のように思考し、証明を導き出す技術が進んでいます。国際数学オリンピックの問題を解ける精度まで向上しており、「AIは数学者になれるか?」という議論も現実的になってきました。学習の場面においても、AIと相談しながら試行錯誤したり、学習のサポート役を任せたりする等、幅広く活用されています。
一方で、理系の人材不足が課題となっています。数学と社会・職業との関係の理解が不十分という指摘を受けて、算数・数学の学習指導要領改訂に向けた議論の中では、高等学校の必履修科目「数学Ⅰ」の中に、現実事象と数学を結び付けて考える「社会を読み解く数学(仮称)」や、数学と社会や職業との関係を学ぶ「数学ガイダンス(仮称)」の追加が検討されています。
今回は算数・数学を生かした仕事と、試行錯誤して学ぶことの大切さについて紹介します。
理系人材の不足
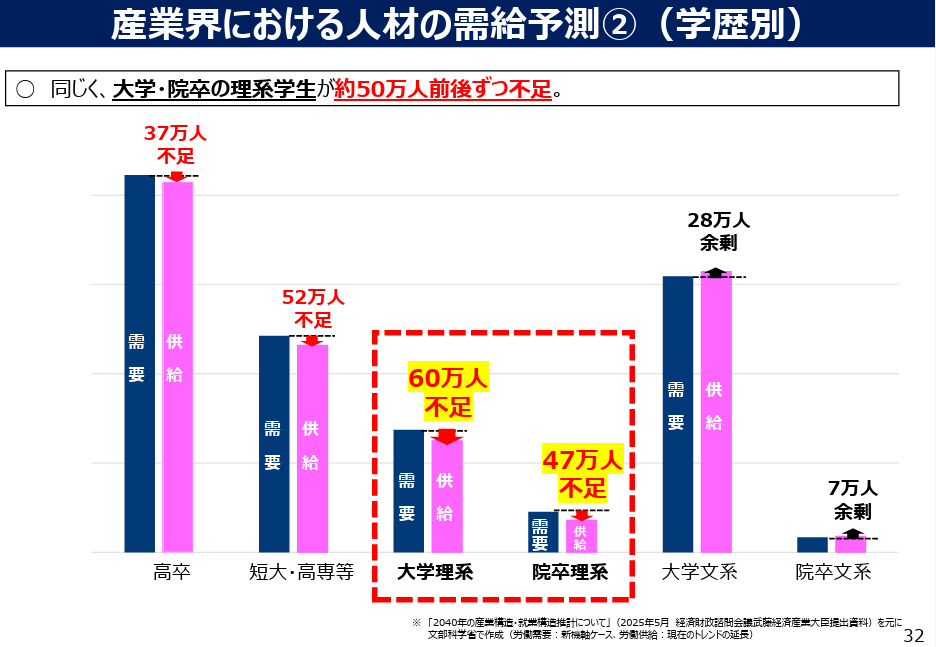
文部科学省の学習指導要領改訂に向けた議論の中では、理系の人材不足が指摘されています。図のように、2040年には約100万人の理系人材が不足されると予測されています。
理系を選択しない原因の一つとして、理数系科目と社会との関係の理解が進んでいない可能性があります。数学がどのように仕事や日常生活と関わっているのか、児童生徒にはイメージしづらいかもしれません。
数学を生かせる仕事
表のように、数学が得意な人の活躍が期待される仕事は沢山あります。
| IT系 | ITエンジニア | 金融・保険系 | 公認会計士 |
|---|---|---|---|
| システムエンジニア | ファイナンシャルプランナー | ||
| プログラマー | 税理士 | ||
| AIエンジニア | ファンドマネージャー | ||
| データサイエンティスト | アクチュアリー | ||
| 教育・研究系 | 数学教師 | 技術系 | 建築士 |
| 数学者 | 技術系エンジニア | ||
| 物理学者 | |||
| JAXA職員 | |||
例えば、AIエンジニアはAIを開発したり改修したりする仕事で、数学はAIの仕組みを理解して設計するために必要となります。アクチュアリーは数学の中でも確率・統計を活用して保険のマネジメント等を行う仕事で、私も目指していた職業の一つです。数学教師や数学者はまさに数学を教えたり研究したりする仕事です。私も数学の講師として働いた経験があります。建築士は、主に設計の場面で数学・物理学の知識が求められます。CAD(Computer Aided Design)と呼ばれるソフトを用いた設計が一般的となり、コンピュータのスキルも要求されます。
また、数学の理論を正しく説明できる能力は、他の場面でも重宝されます。私は学力テストをIRT(項目反応理論)と呼ばれる理論に基づいて分析する仕事に携わっており、分析結果を理解して説明するために数学の知識を活用しています。
日常生活に生かされる数学
では、数学のどのような内容が日常生活に使われているのでしょうか。例えば生成AIでは、入力した文字や画像、音声データ等を数字で表したり、次に来る文字等を予測するために確率を計算したり、誤差を計算してAIの性能を改善したりするために、数学の理論が活用されています。特に誤差の計算には、高等学校の数学Ⅱで習う微分を使います。ボールの動きを使った例で紹介します。
図1のように、谷になっている斜面に向かってボールを転がす状況を想像してください。最も深い位置にたどり着いたらゴールとします。
図2のように、ボールは左右にゆらゆらしながら、だんだん振れ幅が小さくなって、いずれ谷底で止まるでしょう。
もしくは、最初に転がす勢いが強すぎて、図3のように勢いよく飛び出してしまい、より深い(ゴールに近い)谷底を探しに向かうかもしれません。
実は、このボールの動きとAIのアルゴリズムは非常に似ています。
今度は図4のように、斜面がどのような形をしていて、谷底がどこにあるか分からないものとします。
ここで、ボールは急な斜面では大きく、なだらかな斜面では小さく動きます。すなわち、傾き具合(勾配)を調べることで、今、谷底に近いか遠いかが分かります。傾きが急であれば大きく動き、傾きが緩やかであれば小さく動くことで、形が分からなくても、効率的に谷底に近づくことができます。さらに、どちらに傾いているかがわかれば、左右どちらに動けばよいかもわかります。傾いている方向と傾き具合の両方を表しているのは、接線の傾き、すなわち微分係数です。
-
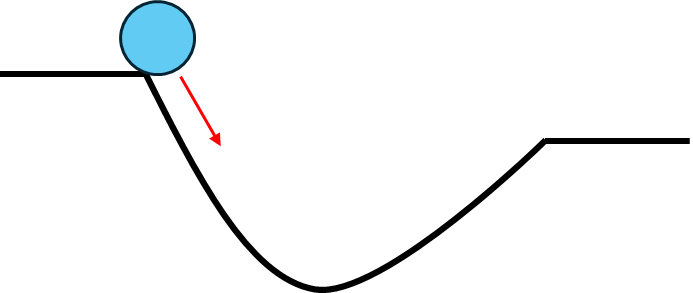
図1
-
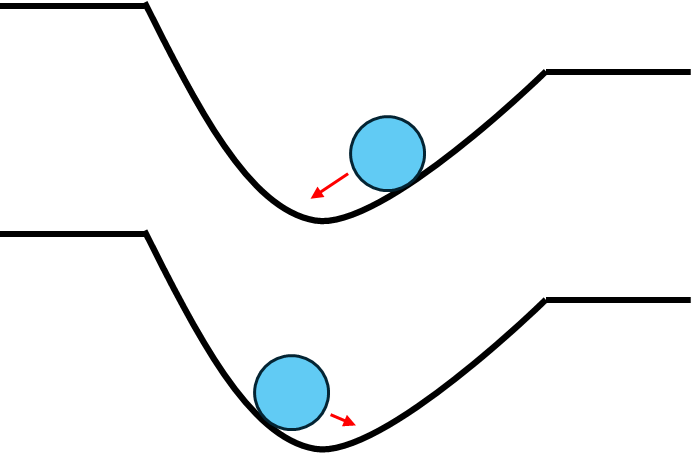
図2
-

図3
-
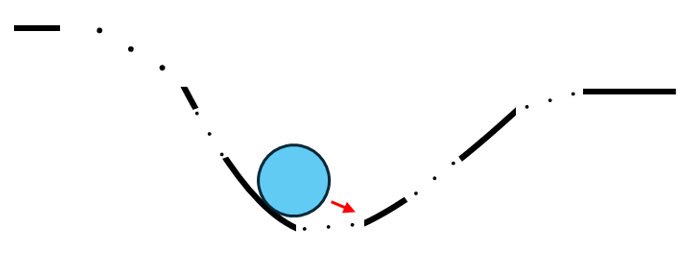
図4
AIでは、出した答えがどの程度希望に沿ったものかを誤差として計算します。AIの性能を上げるためには、誤差を可能な限り小さくする必要があります。
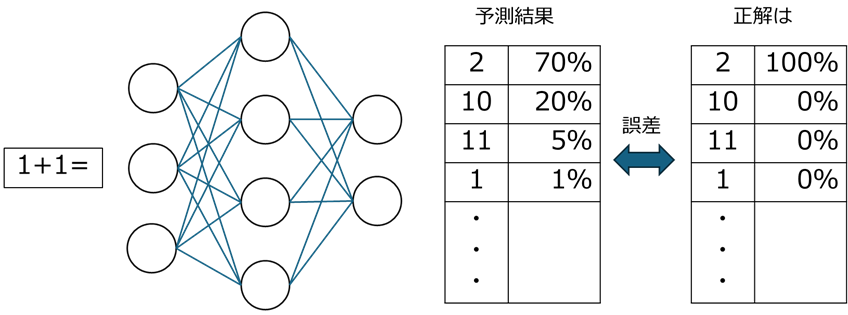
誤差は、誤差関数と呼ばれる複雑な関数で評価され、最も小さくなる場所、すなわち最小値を求める操作を行って性能を改善します。誤差関数はもはや目で見て最小値がわかるものではないので、勾配を利用して谷底へ降りていくアルゴリズムを用います。これを「勾配降下法」といい、機械学習や生成AI等で一般的に用いられる手法です。
日常生活に結び付けて試行錯誤する力
生成AI等の最先端技術が発展する中で、それらをブラックボックス化せずに、仕組みを理解しながら活用することが求められます。学習指導要領改訂の議論においては、生成AIの仕組みを学校段階に応じて学ぶことが検討されています。その際は、日常生活と結び付けて試行錯誤することが重要です。
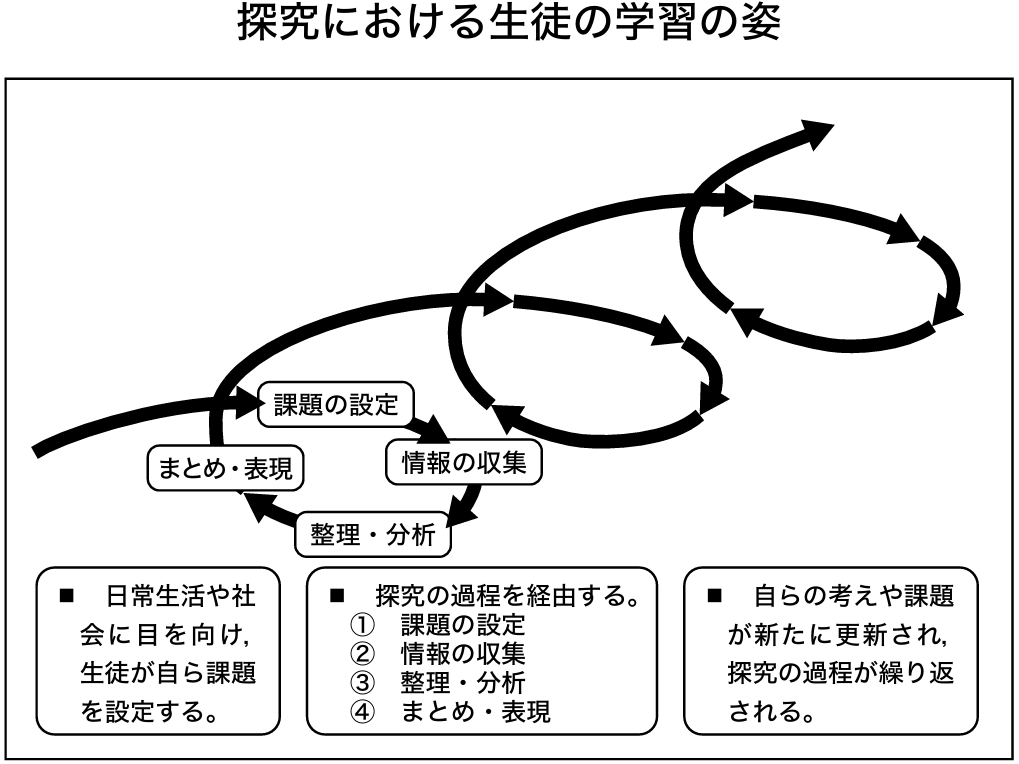
学習指導要領では「探究における生徒の学習の姿」をらせんのイメージで説明しています。
「探究における生徒の学習の姿」とは、日常生活や社会に目を向けて、生徒が自ら課題を設定し、探究の過程の中で解決していく姿です。同学習指導要領は探究について、次のように述べています。
”要するに探究とは,物事の本質を自己との関わりで探り見極めようとする一連の知的営みのことである。”
日常生活の中にある素朴な疑問を数学的に解釈したり、数学の内容を日常生活に当てはめたりして、知的好奇心から学び続け、試行錯誤しながら探っていく力が求められていると考えられます。
認知負荷のコントロール
ではなぜ試行錯誤が重要なのでしょうか。『算数文章題が解けない子どもたち―ことば・思考の力と学力不振』(今井むつみ他 岩波書店・2022)では、つまずく原因の一つとして「推論と認知処理能力の問題」を取り上げています。今井氏は「認知処理の負荷をコントロールしながら推論をする力」が不足していること指摘しています。つまり、補助線を引いたり、文字や図形で置き換えたりして、試行錯誤する中で、わかっていることを明確にし、逆に今考えなくてよい部分のリソースを節約する力が必要だと考えられます。
補助線を使った問題として、面白い問題があるので紹介します。図6の点線部分の面積を求めてみましょう。
これは外の円の半径をR、内の円の半径をr、円周率を\(\pi \)として、
-
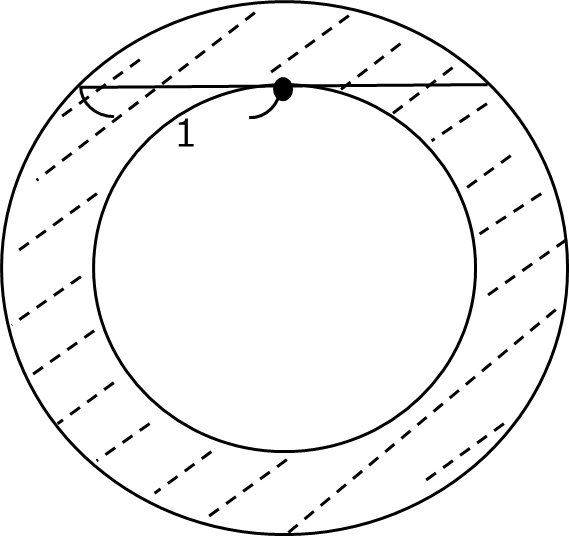
図6
-
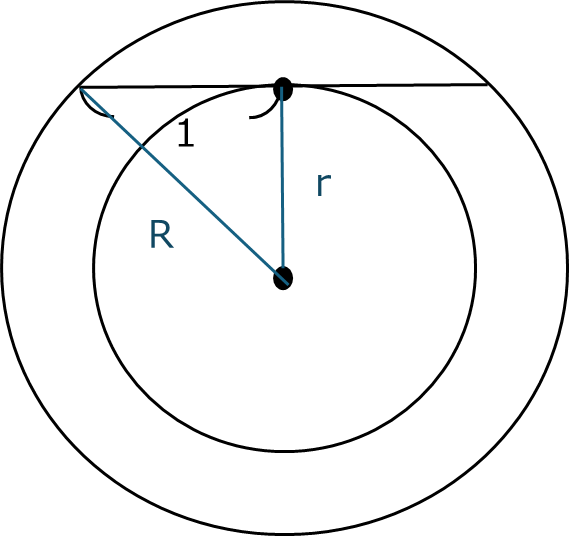
図7
ここで、三平方の定理から
この問題の面白いポイントは、円の半径や面積が分からなくても解けてしまうところです。ただし、補助線をどこに引くかがカギとなり、試行錯誤する力が問われます。人によっては、そもそも補助線を引くという発想に至らなかったり、「効率的に解くためにパターン化したい」と考える人がいるかもしれません。とはいえ、どんな問題に対しても必ず正攻法があるわけではないのです。ここで重要なのは、「何が分かっているか」と「何が分かればよいか」を明確にし、認知負荷をコントロールしながら試行錯誤することです。
証明問題で育成する力
認知負荷をコントロールしながら、見通しを立てて試行錯誤することは、特に証明問題において重要です。
中学校2年生では図形の証明問題を学習しますが、見通しが立っていない状態で試行錯誤しても証明できないことがあります。これまでの「答えを求める問題」とは異なり、「最初から答えが分かっている」点が難しいポイントです。「答えを知らなかったもの」として考える必要があり、メタ認知能力も求められるため、つまずきやすい分野の一つではないかと思います。
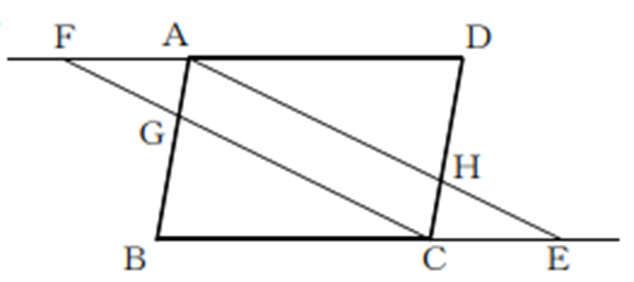
図5は令和7年度全国学力・学習状況調査で出題された、平行四辺形の証明問題です。この問題の無解答率が31.2%であり、他の問題に比べて高い傾向にありました。
※問題内容:四角形AGCHが平行四辺形であることを証明しなさい。ただし、四角形ABCD、四角形FCEAは平行四辺形です。
報告書の解説には、次のように書かれていました。
「事柄が成り立つことを証明できるようにするためには、仮定や仮定から分かる事柄、結論を導くために必要な事柄を明らかにするなどして証明の方針を立て、その方針を基に推論の過程を数学的に表現できるように指導することが大切である。」
つまり、「何をすればゴールなのか」、「材料として何があるのか」、「何が足りていないのか」を明確にし、表現できることが大事なのではないかと思います。
新たな視点の発見
試行錯誤することで、新たな発見につながることもあります。特に数学は、答えが一つに決まってしまうイメージや、なんだか完璧な学問のイメージがあると思いますが、実はそうでもない部分もあります。例えば、小学校では0で数字を割れないと習いますが、分野によっては0で割ることを認める場合もあります。他にも、当たり前のようで証明できていないことも数多くあります。
例えば、未解決問題として有名な「コラッツ予想」は、小学生でも理解できるような予想です。NHKのテレビ番組の「笑わない数学」でも取り上げられていました。
「コラッツ予想」とは、
- 奇数であれば3をかけて1を足す
- 偶数であれば2で割る
この操作を繰り返せば、どんな数もいつかは1になるという予想です。
5→16→8→4→2→1
12→6→3→10→5→16→8→4→2→1
のように、どんな数から始めても、1になります。ただし、本当に全ての数で1になるかは分かっておらず、その証明は非常に難しいとされています。(こちらのサイトでシミュレーションできるので、やってみてください。)
このように、簡単に思いつきそうなものでさえ未解決で、思ったより不完全なところがあります。この不完全さを面白いと感じたり、別の視点を見つけたときに面白いと感じたりできるようになれば、数学を好きになるのではないかと思います。
私は小数の掛け算の「ひっ算」を初めて習ったときに、足し算のひっ算と同様に、小数点の位置を揃えて計算するのではないかと考えました。
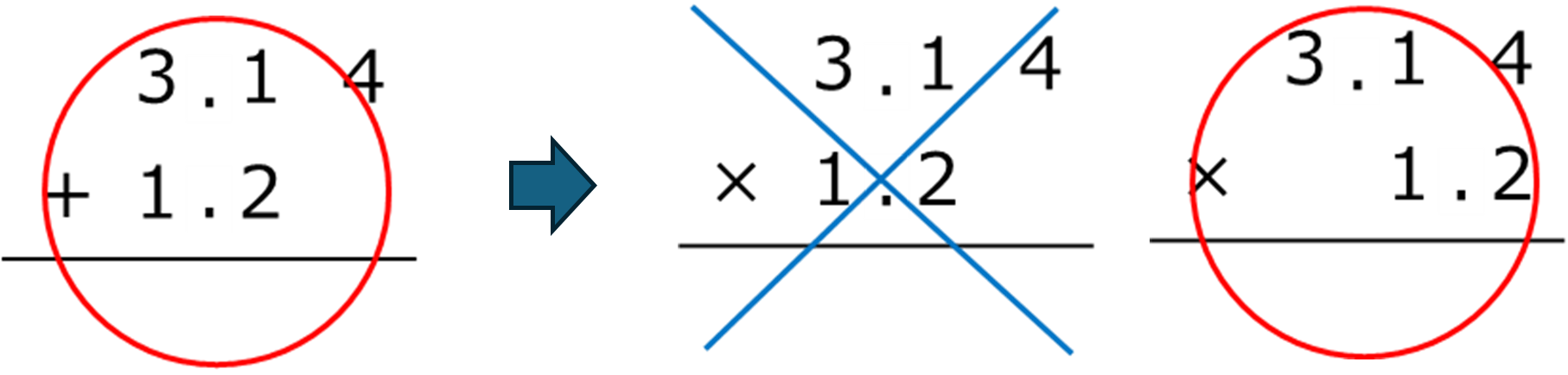
掛け算の場合は右端を揃える必要があるため、小数点を揃える方法は誤りですが、先生にはよく褒められました 。子どもの自分としては、足し算と同じだろうという、単純な考えでした。既習事項を使ったことに対して評価されたのかもしれませんが、先生からは「そういう考え方もあるのか」と言われました。試行錯誤することで、新たな視点を発見することも、学びにおいて貴重な経験なのではないかと思います。
まとめ
最先端技術の進歩に伴い、理系人材の需要はますます増えると予想されます。人材不足の解消に向けて、数学と社会・職業との関係の理解を進めていくことが必要だと考えられます。
また、数学を日常生活と関連付けて、試行錯誤しながら解決していくことが大切です。試行錯誤する際は、見通しを立てられるように指導していくことが求められます。試行錯誤する中で、新たな発見が生まれることもあります。数学のつまずきポイントを押さえて、一緒に解決していくことで、数学を好きな子どもたちが増えるとよいなと思います。
参考資料
構成・文:内田洋行教育総合研究所 研究員 橋本 真隆
※当記事のすべてのコンテンツ(文・画像等)の無断使用を禁じます。
ご意見・ご要望、お待ちしています!
この記事に対する皆様のご意見、ご要望をお寄せください。今後の記事制作の参考にさせていただきます。(なお個別・個人的なご質問・ご相談等に関してはお受けいたしかねます。)
この記事に関連するおススメ記事

「教育トレンド」の最新記事














 教育インタビュー
教育インタビュー 新刊紹介
新刊紹介 教材紹介
教材紹介



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事 ご意見・ご要望
ご意見・ご要望
