意外と知らない"算数・数学のつまずきポイント"(第1回) 誤ったスキーマが新たな概念の習得を困難にしている可能性
PISA2022の結果によると、日本の数学的リテラシーは世界トップレベルですが、「数学の授業についていけないのではないかとよく心配になる」生徒の割合はOECD 加盟国平均の 59.8%より高い68.8%でした。令和7年度全国学力・学習状況調査報告書【質問調査】でも、算数・数学は他の教科に比べて苦手と感じる児童生徒が多い傾向にあります。そして、中学校から数学が苦手な児童生徒は増える傾向がみられます。第1回では、算数・数学のつまずきやすいポイントと、その原因、解決方法について考えてみます。
濃度計算問題の落とし穴
たとえば、食塩水の計算問題について、苦手意識を持つ子どもたちが多いのではないでしょうか。私も「濃度」や「食塩水」という単語を見ただけで後回しにするほど、苦手にしていました。なぜ苦手に感じやすいのでしょうか。
小学校5年生で習う問題「100gの水に食塩を5g溶かしました。食塩水の濃度は何%ですか。」について一緒に考えてみましょう。
答えは5%・・・ではありません。全体の重さが食塩5g分増えているので、
つまり、正解は約4.76%です。
よく考えれば、食塩は水に溶けて無くなったわけではありません。食塩を入れた分、容器の中身は重くなっています。しかし、パッと見た時に、水100gに対する食塩5gという割合の構図が浮かんでしまいます。最初から水 + 食塩で割る必要があることに気づくのは困難です。また、中には「やはり水の重さだけで割るべきだ」と納得できない子もいるでしょう。直感と異なっていたり、問題文に行間や隠されたねらいがあったりする問題に対して、難しいと感じる子は多いと思います。
いつ算数・数学が苦手になるのか
算数から数学への転換は大きなターニングポイントと言えるでしょう。小学校で分数・小数や割合を理解できた生徒でも、中学校の数学に切り替わると、抽象的になり、直感で捉えにくくなるため、つまずくことが多いようです。例えば、令和7年度の全国学力・学習状況調査の結果から、国語と算数・数学に対する意識の変化を比較してみます。
国語が得意だと答えた割合は、「当てはまる」「どちらかと言えば、当てはまる」を合わせて、小学校:61.6%、中学校:51.6%です。一方、算数・数学が得意だと答えた割合は、小学校:60.3%、中学校:46.2%程度で、国語よりやや低く、特に中学校は半分以下という結果が出ています。
算数に比べ、数学で「当てはまる」と回答した割合は11.7%も低く、算数から数学になった段階で、算数・数学が苦手な児童生徒は増える傾向にあると考えられます。また、国語と比較して、小中どちらも得意な子と苦手な子がはっきり分かれているようにも見えます。
なぜ数学が苦手になるのか
なぜ中学校から数学が苦手な生徒が増えてしまうのでしょうか。石川・立花(2019.3)の論文「学習意欲が低い生徒も学びに向かえる授業の構成―中学生における数学嫌いの要因を基にー」では、「数学嫌いと自己暗示をかけることで、学習意欲が下がってしまう」という課題を取り上げています。
冒頭で述べたように、日本は世界トップレベルの数学力を持っていながら、「数学は苦手だ」と認識している割合が高いです。これは、謙虚に答えているだけの可能性もありますが、セルフ・ハンディキャップの戦略を使っている可能性もあります。つまり、本当は苦手でも何でもないのに、苦手と言っておけば、「苦手だからできなかった」「苦手なのにできた」という、どちらに転んでも言い訳できる準備をしているということです。
こうした戦略をとる理由としては、数学特有の難しさが関係しているのではないかと考えられます。上記の論文では、数学嫌いの要因に関するアンケート調査結果を下表のとおりまとめています。
| ①数学固有の特質 | 1. 特定 | 「計算」や「文字式など具体的単元」が苦手 |
| 2. つまずき | 一度つまずいたあと立て直せない。 | |
| 3. イメージ | 解法がひらめかない。図形など頭でイメージできない。 | |
| 4 . 解が1つ | できないことが目に見える。点数がとれない。 | |
| 5. 言葉 | 聞かれていることを理解できない。文章から立式ができない。 | |
| 6. 公式 | 暗記していないとなにもできない 。 | |
| ② 授業の 進め方 | 7. 有用感 | 日常生活への応用の実感がない。 |
| 8. 形式指導 | 答えは分かっても理由が分からない 。 | |
| 9. スピード | できる人の発言で授業が進む。 |
私は高等学校で数学の講師として働いた経験がありますが、数学が苦手な生徒の中には、「6.公式」のように暗記しなければならない部分があるが、他教科と比べてコストパフォーマンスが悪く、勉強を負担に感じる生徒や、「7.有用感」のように何に役立つのか分からないから勉強を避けたがる生徒もいました。数学が得意な生徒でも、「3.イメージ」のようにテストで解法が思いつかないことを懸念していたり、「8.形式指導」のように最初から理解することを諦めて形式的に解く方法で対処したりする生徒もいました。例え得意であっても、概念をしっかり理解した上で学習を進めることは難しいようです。
つまずきの原因
それでは、なぜ概念を理解しながら学習することは難しいのでしょうか。一つは、内容が抽象的になっていく中で、自分の中にある既存の概念と食い違うことが原因ではないかと考えられます。 『算数文章題が解けない子どもたち―ことば・思考の力と学力不振』(今井むつみ他 岩波書店・2022)では、「スキーマ」という言葉を次のとおり定義しています。
これまでの生活経験や学習経験の中で素朴に培ってきた、枠組みとなる知識のことを認知心理学では「スキーマ」とよぶ。
スキーマとは、例えば水を入れる容器が何かと問われれば「コップ」と答えられるように、無意識に人が持つ認識のことです。今井氏は、人によってスキーマが異なり、誤ったスキーマを持った状態で新たな概念を習得することは困難だと述べています。
例えば、中学校1年生の文字式の分野で、同じ文字は同じ数字だから、次のように表すことを習います。
つまずきへの対応方法①
では、児童生徒がつまずいたとき、どう対応すればよいでしょうか。一つは、常に誰しも誤ったスキーマを持っていると考えることだと思います。これは児童生徒に限らず教える側にも、認識に誤りを含む可能性があることを念頭に置いた上で、説明・理解していく必要があると考えます。すなわち、「自分や相手の理解の仕方自体が、間違っているかもしれない」という考えを持っておくということです。
例えば、大学数学では「写像」という概念を学びます。写像は、簡単に言えば関数みたいなものですが、関数をより拡張した概念です。次の関数について考えてみます。
この𝑓(𝑥)は、𝑥 = 1のとき2、𝑥 = 2のとき3のように、 𝑥が一つ決まれば𝑓(𝑥)も一つに決まります。このような𝑓(𝑥)を関数といいます。数字に限らず、一つを決めれば一つに定まる対応関係を表すものを写像といいます。次の例も写像です。
𝑓:きゃべつ→野菜
𝑓:みかん→果物
上の写像は、一つの食べ物に対して一つの種類を対応させる写像です。この写像は、「りんご」と「みかん」は同じ果物で、「きゃべつ」のみ野菜に分類されることを表しています。この写像の特徴を数学の用語で「全射であり単射でない写像」といいます。
全射とは、矢印の行き先を全て網羅していることを意味します。今考えている種類が果物と野菜しかなく、どちらも網羅されているため、この写像は「全射」という特徴を持っています。単射とは、全ての矢印の行き先が重複しないことを意味します。つまり、りんごとみかんは同じ果物で被っているため、「単射」ではありません。
したがって、「全射であり単射でない写像を作成せよ」という課題に対して、上のような写像を作成すればよいです。しかし、先に述べた「写像は関数のようなもの」という概念を誤って認識した結果、どうにかして関数で表そうとする可能性があります。これは、誤ったスキーマで考えてしまうことと、そのスキーマを見直せないことが原因だと考えられます。常にスキーマ自体が間違っている可能性を考慮することで、新たな世界観へアップデートできるチャンスが増えると思います。
つまずきへの対応方法②
もう一つは、具体化することです。算数・数学は学習が進むほど、より抽象的な概念へと変わります。そのとき、抽象的なまま進めてしまうと、理解しているかどうかの判断が難しくなります。具体化とは、「例えば○○だったら」という検証を重ねて、行間を埋めたり、理解の補助となるように認知負荷を軽減させたりする手法です。より解像度を広げるために、日常生活の中に置き換えて考えることも重要です。
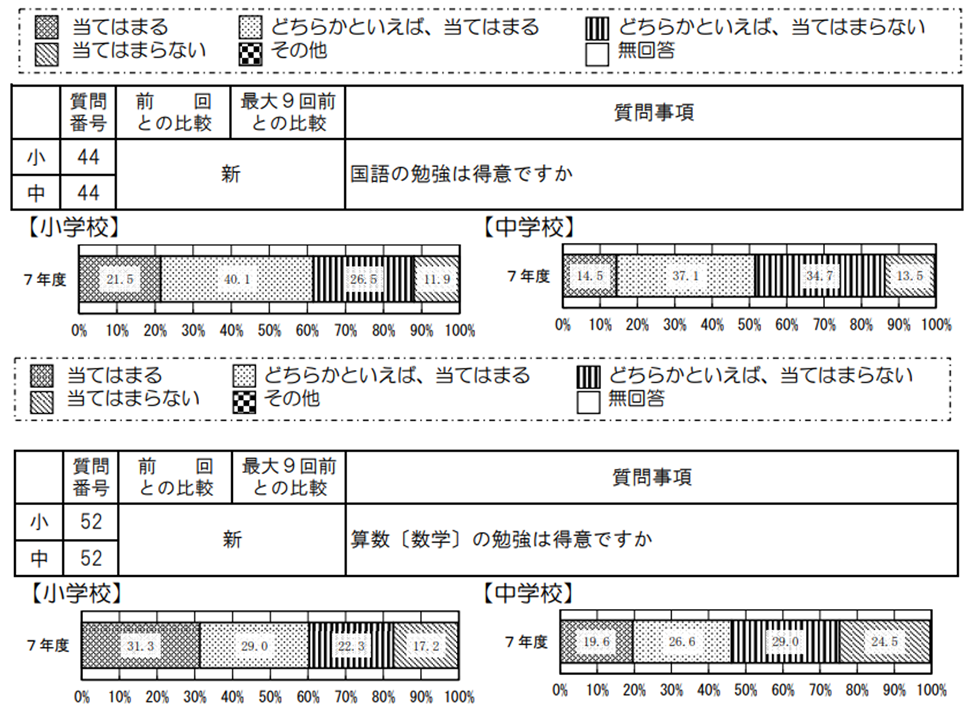
日常生活と算数・数学を関連付けて考えることは、学習指導要領における「算数・数学の学習過程のイメージ」の中に示されています。
ここに示されているとおり、数学的な見方・考え方を働かせながら、日常生活の事象を数学的に処理して問題を解決する力が求められています。特に抽象化が進んでいくと、日常からかけ離れてしまい、一体それが何なのか、何の役に立つのか、学問自体に対する疑問や嫌悪感を抱いてしまう様子も見られます。そこのギャップを埋める役割が教師にあるのではないでしょうか。
具体化の例として、金沢駅の「鼓門(つづらもん)」を紹介します。

金沢駅 鼓門(友人撮影)
-

図1
-
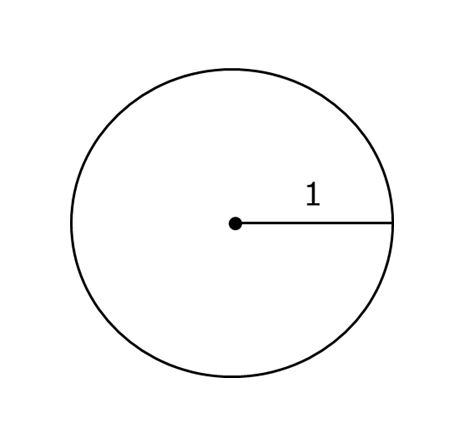
図2
-
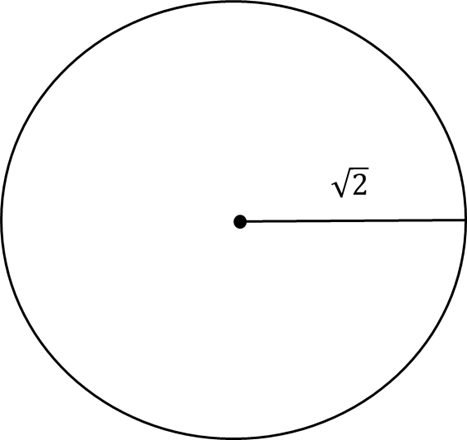
図3
-
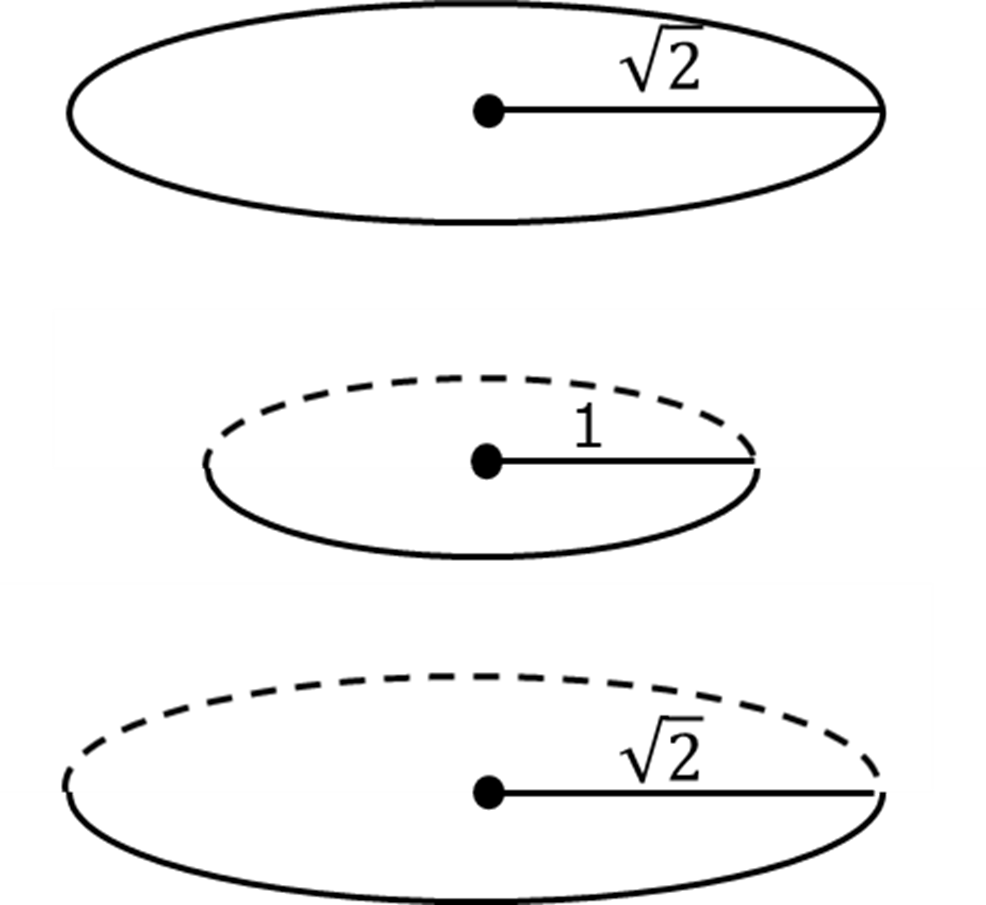
図4
第1回のまとめ
これまでの内容をまとめると、次のとおりです。
- 算数から数学に切り替わる段階で、苦手な児童生徒は増える傾向にある。
- 数学でつまずく理由は、誤ったスキーマを持った状態で、新たな概念を習得することは困難だからだと考えられる。
つまずきの対応方法としては、例えば次の2点が考えられる。
①誤ったスキーマを持っている可能性を考慮する
②具体化して、日常生活と関連付けて考える
次回は「試行錯誤して学ぶことの大切さ」と「算数・数学を生かした仕事」について紹介します。
構成・文:内田洋行教育総合研究所 研究員 橋本 真隆
※当記事のすべてのコンテンツ(文・画像等)の無断使用を禁じます。
ご意見・ご要望、お待ちしています!
この記事に対する皆様のご意見、ご要望をお寄せください。今後の記事制作の参考にさせていただきます。(なお個別・個人的なご質問・ご相談等に関してはお受けいたしかねます。)
この記事に関連するおススメ記事

「教育トレンド」の最新記事














 教育インタビュー
教育インタビュー 新刊紹介
新刊紹介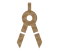 教材紹介
教材紹介



 この記事をクリップ
この記事をクリップ クリップした記事
クリップした記事 ご意見・ご要望
ご意見・ご要望
