サイコロを振る体験を通して、統計的に問題を解決する力を育む授業（前編）

確率の導入として、サイコロを振る活動は教科書等でも紹介され、よく扱われる内容である。一方、生徒は「サイコロは1から6までの目がほぼ偏りなく出る」と経験上認識しているため、実験をすることに大きな意義を見出せず、実験結果に関心をもてないことも少なくない。そこで石綿教諭は、立方体以外のかたちやおもりを入れるなどした自作のサイコロを用意し、実際に生徒に振らせてデータを収集する活動を取り入れることにした。

立方体以外のかたちやおもりを入れたサイコロは、見た目から結果を判断、予想するのは難しい。結果を予想するのが難しいサイコロを取り入れることで、生徒に実験を行う必要性を感じさせるのが本授業の狙いだ。また、立方体以外の形やおもりを入れたサイコロは目の出方の偏りが大きくなると予想されるため、多数回の実験が必要になることも自然と感得できると考えた。

石綿教諭が本授業のために用意したサイコロは全部で10種。いずれも工作用紙を用いて作成したものである。各面はセロハンテープで貼り合わせている。立方体のかたちをしたサイコロの中には、ナットを使ったおもりを入れて目の出方が偏るようにしたものがある。見分けをつけるために、目の色を青にする面をつくり、目印とした。他のサイコロは、１の目が赤、他の目を黒にして作成している。

授業ではまず生徒たちに10種のサイコロを提示し、どのサイコロが1～6までの目が偏りなく出る公平なサイコロであるかを問うところから始まった。

「この中で、公平なサイコロはどれだと思う？」

「四角いもの」
「1〜6まで公平に出るもの」
「立方体のサイコロなら大丈夫」

次に、おもり入りのサイコロを実際に何回か振ってみせる。すると、生徒たちから「このサイコロはおかしい。1の目ばっかり出る」との声があがった。

「確かに1の目ばかり出ますね。どのくらい1の目が出やすいのか調べるために、実際にサイコロを振ってみましょう」

サイコロに偏りがあることを実感させることで初めて、生徒たちは実験を行う必要性を感じる。実験への内発的動機づけを促したところから、サイコロを振る実験がはじまった。

「サイコロを振るにあたって、グループ分けをします。向かい合って2人組をつくってください」

本授業は、20人程の少人数指導学級を想定して行う。本授業における学級の生徒数は18人。2人組×9グループで実験が行われることとなった。もし40人学級で行う場合は、同じ条件のサイコロを２つずつ用意して2人組×20グループで授業を行うことをおすすめする。

「いまからグループごとに、実験結果を記録するワークシートを配ります。振ってもらうサイコロは全部で10種類。それぞれのグループで1個ずつサイコロを分担し、それぞれ30回ずつ振ってください。グループ内の役割分担としては、1人がサイコロを振り、1人がワークシートに記録します。30回振り終わったら、グループ1は1番のサイコロをグループ9にわたしてください。グループ1はグループ2から2番のサイコロが回ってくるので、それを振ります」

導入からグループ分けまでで、約10分が経過。

「それでは、どのサイコロが一番正確にまんべんなく出るのかを確かめてみましょう」

生徒たちは1秒に2回くらいのペースで、1個のサイコロにつき30回ずつ振り続ける。10個のサイコロを振り終えるのに15分ほどかかった。

「いったん作業を中止してください。次はサイコロごとに1〜6の目がそれぞれ何回ずつ出たかを計算します。1番のサイコロは何回出た？」

「6、6、2、9、3、4」

「まったく同じだったグループはあった？　ないよね、そういう感覚も大事です」

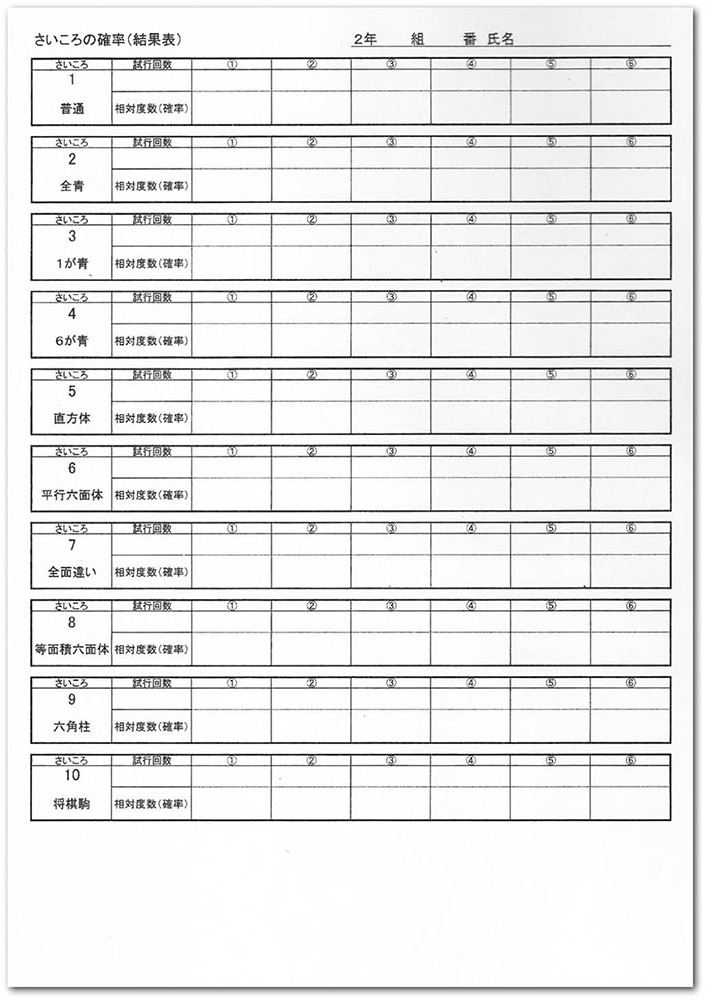
使用したワークシート

ここで各グループに計算機が配られる。相対度数を計算するためだ。

「相対度数って覚えてる？　たとえば30回振って、1の目が6回出たなら、6÷30 で0.2 が相対度数になります。2÷30のように割り切れないときもあるので、その場合は小数第3位を四捨五入してください」

相対度数の計算をはじめておよそ15分後。まだ計算を終えていない生徒も多いが、残り少ない授業時間を考えるとここで切り上げざるをえない。

「あと1〜2分したら発表してもらおうと思うので、自分のグループの番号を優先して計算してください」

「では、途中のところもあるかもしれないけど、いったん作業を終わりにします。グループごとに相対度数を発表してください」

全グループが発表し終わったところで、気づいたことを発表させる。

「こうやって数値を見ていくと、サイコロとしてかなり偏っているものがあるのが分かりますね。どのサイコロが一番偏っていた？」

「10番」

「そうですね。将棋のコマは見た目にも偏りがあるし、実際に振ってみてもやはり偏りが大きかったですよね。あと、3番も偏りが大きいよね。実際に振ってみて、『6が出やすい』という判断もできたと思います。逆に、割とまんべんなく出たというサイコロは何番？」

「１番」

「そうですね。こうやって実験をしてみると、1番のサイコロは偏りのない公平なサイコロであることが分かります」

各グループがすべてのサイコロを振り終えると、学級全体でのそれぞれのサイコロの実験回数は、30回×9で270回になる。

「時間がなくて全部のサイコロではできませんでしたが、1番と2番と3番のサイコロについて、学級全体の実験結果を合計してみました。1番のサイコロはだいたい割合がそろっているかな。2番のサイコロもそこそこそろっています。3番のサイコロには6の目が出やすい傾向がありましたが、全体の合計を足してみても、やっぱり6割近く6の目が出ました。このように、たくさん振る実験をしていくと、サイコロの各目がどのくらいの割合で出てくるのかというのは次第につかめるようになります」

データの分析を行うにあたって、270回分のデータは、1回の授業内の実験で収集できる量としては十分だろう。ただ、50分の授業内に実験結果をまとめ、そこからデータの傾向を調べるところまでもっていくのは時間的に困難だ。本授業の最終的なまとめは、次回の授業への持ち越しとなった。

「次回は学級全体の実験結果の合計から、相対度数を求めていきます。自分のグループの記録と学級全体の記録を比べることで、新しい発見があるかもしれません」