アグネスの教育アドバイス
映画と教育
震災を忘れない
愉しい授業を創る 私の考えを超えていく子どもの考えを愉しむ編
子どもも、教師も「愉しい」授業は、どのように創ればよいでしょう？
教師が愉しめなかったら、多分、子どもも愉しくないのではないかと思います。
だから、まず教師が愉しむことですね。楽しむではなくて、愉しむってことです（もちろん、明るく、柔らかい空気を創り出すことは、必要なので、楽しさも必要だと思います）。
私の場合の愉しみは、子どもと教材の相互作用によって起きる反応（？）です。
浜松学院大学地域共創学部地域子ども教育学科 教授 川島 隆
指導案を創るということの取組
私が、大学で前期に担当している科目の1つに、「初等教科教育法（算数）」があります。
これは、いわゆる指導法の授業で、その教科の指導に関する内容を演習を通して学んでいきます。
私の場合は、全15回の授業のうち、前半７回程度を私の示範授業を含めての講義中心、後半７回程度を学生による模擬授業の実施とそのリフレクション（振り返り）を中心に、最後１回を総括に当てています。
前半では、領域ごとの指導の要点を学生相手の示範授業をしながら、具体的な教材をもとに伝えていきます。
つまり、私が授業者、学生が子ども役となって授業を展開していくのです。
学生は、算数科の教材の特性とともに、目標、めあて（課題）、予想される子どもの反応、まとめ、評価など指導案に記す内容を具体的にイメージしながら活動します。
そして、その授業後、今まで行われてきた授業を振り返って指導案に書き起こしていきます。
学生は、たった今、自分が受けた授業を、自ら体験をもとに、紙面に書き表していくという活動をするのです。
それでも、指導する側に立つという、これまでとは全く逆の立場に立って物事を考えるということ、言語化するということは、そんなにたやすいことではないようです。
ただ領域は違っても、繰り返し授業を、指導案に書くという経験をすることで、指導案を書くということの意味や書き方を理解していくのだと思います。
皆さんは、どのようにして指導案について学んできたでしょうか。
円の面積の示範授業で
さて、第４回図形領域を扱った授業のときのことでした。
教材は、第6学年「円の面積」です。
授業後半の、示範授業で、私が提案した問題は、次の通りです。
大きさも値段も異なるAとBの2つの円形のタルトがあります。
どちらを買うとお得でしょうか？
まず、それぞれのタルトの大きさ（面積）が分からないと、どちらが得か(面積あたりの値段が安いか)が求められません。
ここで、タルト（円）の面積を求めるという必然性が子どもの中に生まれます。
この問題では、タルト（円）の大きさ（面積）を求めて終わりではなく、そこから単位量あたりの大きさの考えを生かして1平方センチメートルあたりの値段を求め、比較すること、その値段がA、Bのいずれが安いかを判断することまでが求められています。
そこに、この問題のよさがあると思います。
つまり、子どもは、自らの生活に結びつけながら、しかも、筋道を立てて考え、これまでに学び得た知識を生かして解決にあたることができるのです。
円の面積は、どうやって求めるか
話を元に戻します。
タルト（円）の面積を求めるにあたって、はじめタルトを16等分します。
そして、その16等分した扇形を並び替えることで、タルト（円）の面積を求めていきます（図1参照)。
その結果として、円の面積の公式を導き出すことを目指しています。
したがって、この授業のポイントの1つは、扇形をどのような形に並べるか、円をどう変形するかというところです。
教科書によると、算数科を扱っている全6社すべてが、最終的には長方形に帰着させています。
ただ、16等分にした扇形では長方形にはならず、長方形と考えるには無理があり、平行四辺形と考えるのが妥当ではないかと思われます。
どの教科書も、円を16等分から32等分へ、さらに細分化して、64等分することで、長方形とみなすことができるとしています。
学生が作った形は、
ここでは、そのことには触れず、子ども役の学生は、16等分した扇形をノートに貼り合わせていきます。
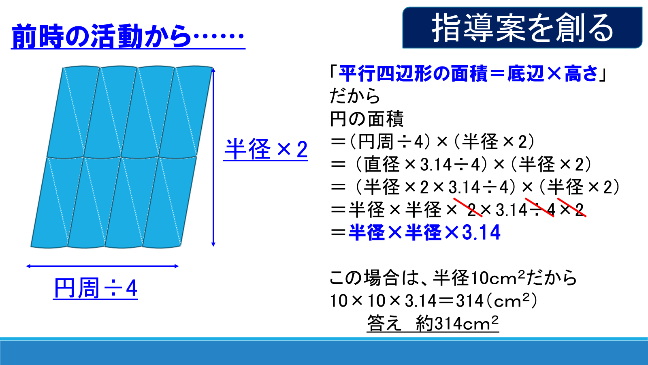
結果をみると、学生が作った形は、ほぼ全員が平行四辺形でした（図２参照）。
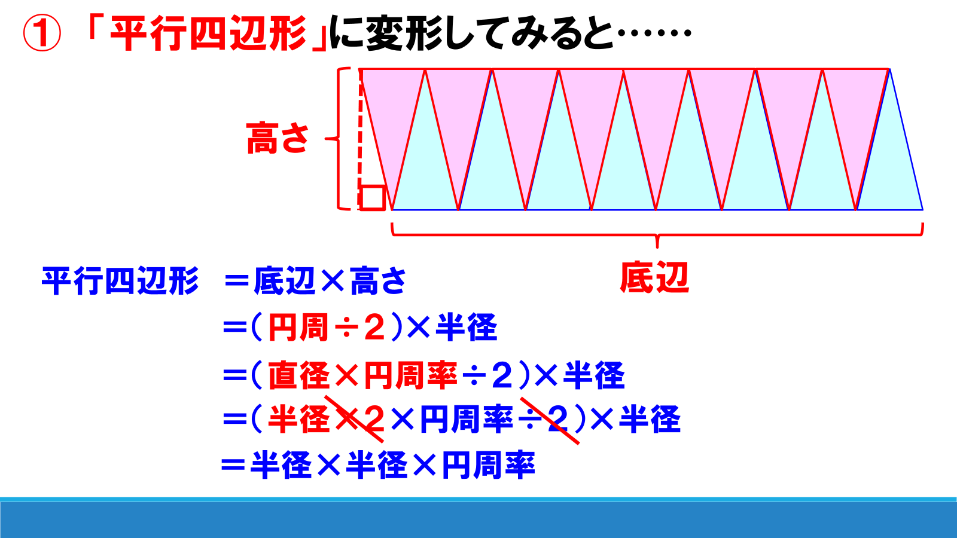
そして、平行四辺形の面積の求め方（「底辺」×「高さ」）を活用して、円の面積の公式につながっていくことを確かめました。
丁寧に式をつないでいくと、何故円の公式が導かれたかが分かっていきます。
子どもの考えは、多様であること
何故、皆がそろって、平行四辺形にしたかは、分かりません。
私からは、子どもたちの考え方は多様であり、指導する側も多様な意見が出されることを想定しておくことが必要であることを伝えました。
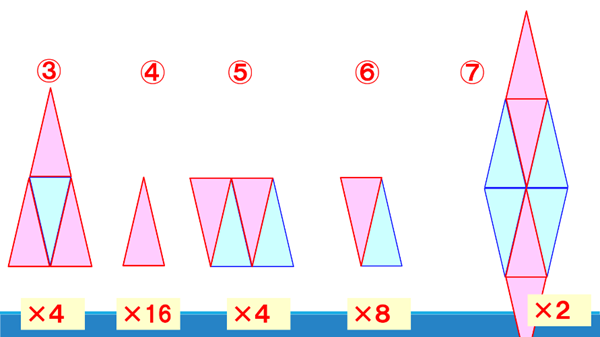
そして、私が提示したのは、図３です。
平行四辺形で同様に、三角形でも円の公式が最終的には導かれていきます。
（ちなみに、この三角形への変形を扱っている教科書会社は、１社のみです）
教師にとっての授業の「愉しさ」は
そして、その次の授業で、この時間の「振り返り」を紹介しながら、図4のような求め方も紹介しました。
ただ、この考え方を含めたとしても、３つの考えにすぎません。
子どもの考えは、これだけでしょうか。
子どもなら、もっといろいろな考えをしてくるんじゃないでしょうか。それらを「予想すること」に、教師にとって一つの愉しさがあるのではないでしょうか。
どんな考えを出してくるのだろうと。
教師の予想だにしない考え方に出会ったとき、ちょっぴり悔しくて、嬉しくて、驚いて、感心して、納得する。
そんなことを感じたことはないでしょうか。
教師にとっての授業の「愉しさ」は、そんなところにもあると思います。
学生の「振り返り」から考えること
この授業を通して、学生は、次のような振り返りをしています。
その一部を紹介します。（図5参照）
このような授業でまとめの中で子どもに見られがちなのは、
「円の面積の求め方は、
『半径×半径× 3.14』を計算すればよい」
というものです。
しかし、私が大切にしたいのは、この公式という結果ではなく、経過プロセスです。
思考のプロセスです。
「How」子ども自身がどのように考えたのか、どのようにして公式を導き出したのか、どのように思考を働かせてきたのか、これこそを大切にしたいと思うのです。
まとめには欠かせないと思うのでした。
そして、そうした「How」を大切にしていくには、多様な考えを交流させる場やそれらを組織する教師の力量、さらに、あらかじめどのような考えが生まれてくるかを予想する教師の教材研究や教科書研究が重要な意味を持ってくると言えます。
実際の子どもの考えは、……
子どもたちの考え
そういえば、昨年度A小学校6年生と「円の面積」を学習したことを思い出しました。
その授業をあらためて振り返り、子どもたちはどんな思考を巡らしていたかをみてみましょう。
私があらかじめ想定していたのは、大きく3つほどでした。
もちろんこれ以外にも、出てくるだろうと想定はしていました。
で、実際にはどうであったかと言うと、3つどころではありませんでした。
実際に、子どもたちから出てきた考えは、図5に示す通りです。
これだけ出てくると、1時間の授業では、とても収めることはできません。
2時間扱いに変更せざるを得ませんでした。
でも、それは子どもたちが一生懸命考えて生まれた授業なので、大切にしたいと考えました。
むすびに
指導案に子どもの反応を書いていくと、実際の授業では（特に、公開する授業では）、どうしてもそこに拘りがちです。
しかし、当然そこに収まりきれない、多様な子どもの考えが生まれてきますし、中には、どう対応したらよいかわからず、右往左往する、立ち止まってしまう、
そんな場面も出てくることがあります。
授業者としての私は、今、どうすべきか、子どもたちにどう働き掛けるのがよいのかなど、様々な思いが頭の中で錯綜して、焦りにも似た感情が湧き起こってくることもあります。
しかし、今は、授業を行う前に、それまでの子どもの学び、子どもの生活や子どもの経験を想起し、予想してみる。
どんな考えが生まれてくるのか、できる限り出してみる。
すると、ちょっぴりゆとりが生まれてくるかもしれないと考えています。
また、むしろ、準備はするけれど、私の考えを超えていく子どもの考えをむしろ愉しみに授業をしてみようと思います。
昨年度の授業は、そんな心持ちで、授業に取り組んでいました。
つまり、大切なのは教師の考えに子どもを押し込めない、教師の考えで授業を引っ張っていかない。
教師の考えを超えた子どもの考えに驚きや関心の目を持って対応できる。そんな教師の構えが大切なのかなと思っています。
川島 隆（かわしま たかし）
浜松学院大学地域共創学部地域子ども教育学科 教授
2020年度まで静岡県内公立小学校に勤務し、2021年度から大学教員として、幼稚園教諭・保育士、小学校・特別支援学校教員を目指す学生の指導・支援にあたっています。幼小接続の在り方や成長実感を伴う教師の力量形成を中心に、教育現場に貢献できる研究と教育に微力ながら力を尽くしていきたいと考えております。
この記事をクリップ
クリップした記事ご意見・ご要望、お待ちしています！
この記事に対する皆様のご意見、ご要望をお寄せください。今後の記事制作の参考にさせていただきます。（なお個別・個人的なご質問・ご相談等に関してはお受けいたしかねます。）
ご意見・ご要望「教育エッセイ」の最新記事
