| ねらい |
等差数列の和について考える。 |
| 対 象 |
高学年 |
| 準備するもの |
キズネール棒 |
| 活動の流れ |
指導上の留意点 |
 |
問題を把握する。
１＋２＋３＋４＋……＋100の答えはいくつになりますか。
|
|
 |
問題をやさしくした場面で考えさせる。
・１から10までの計算だったらどうかと考えさせる。
|
|
 |
１から10までの場合をキズネール棒を使って考えてみる。
|
|
 |
いろいろな方法で考えさせる。
①下の半分を上に移動する方法
１＋２＋３＋４＋５
＋６＋７＋８＋９＋10
＝（１＋10）＋（２＋９）
＋（３＋８）＋（４＋７）＋
（５＋６）
＝11×５＝55
②同じものを逆さにならべて２倍分を考える方法
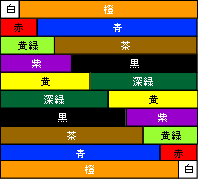
１＋２＋３＋４＋５
＋６＋７＋８＋９＋10
１+２+３+４+５+６+７+８+９+10
＋）10+９+８+７+６+５+４+３+２+１
11+11+11+11+11+11+11+11+11+11
11×10÷２＝55
|
| |
|
 |
１から10までの和を求める方法を使って１から100までの和を求める方法を考える。
①101×50＝5050
②101×100÷2＝5050
|
|
 |
前の２つの方法に対応させて考えさせる。 |
|
 |
発展として１から1000までの和を求める。
①1001×500＝500500
②1001×1000÷２＝500500
|
|
 |
これまでの問題からパターンを見つけさせる。
・１から10までの和 55
・１から100までの和 5050
・１から1000までの和 500500
|
|
【免責事項】
「指導案，授業アイデア，教材・プリント」は、投稿をいただいた学習指導案や事例、手作り教材、アイデア等のコンテンツやサイトをご紹介するコーナーであり、 内容の合法性、正確性、道徳性、最新性、適切性、著作権の許諾や有無など、その内容については一切の保証を致しかねます。当コーナーに掲載されているコンテンツ、または掲載されているリンク先サイトのご利用で発生した損失や損害については、一切責任を負いません。使用および閲覧は利用者の責任において行うものとします。
指導案
授業アイデア
学校で使えるイラスト
校務ツール（書式など）
この記事をクリップ
クリップした記事
指導案 / 授業アイデア / 教材・プリント投稿募集
